flowglow
Mechanical
- Apr 30, 2014
- 14
Hello everyone.
I wanted to make a very simple simulation - compression of cylindrical specimen. I was very surprised, when the solution was not converging.. and it is when more complex models work quiet well.
It is a second day, but still I didn't found completely the reason of this strange behaviour of my model.
Model:
Problem:
Cylinder (Arruda-Boyce hyperelastic model, height = 34 mm, diameter = 34 mm) is compressed between two analytically rigid plates. Axisymmetrical approach is used to solve the problem.
Contact:
between plates and specimen - surface-to-surface contact, with friction coeficient=0.1. Normal behaviour "Hard" or "Exponential" (I tried both).
BC:
Bottom plate is fully fixed, Top plate is going down(displacement BC) in order to compress cylindrical specimen with total 15mm displacement.
Abaqus/Standard:
First of all I started with Abaqus/Standard - problem is static, material is rate independent. Approximately at the middle of a step (~7.5 mm) time increment starts to decrease dramatically and finally reaches the minimum limit. On my opinion, large deformations leads to problem in contact zone, and as a result to very small time increment.
Abaqus/Explicit:
It is well known that generally Explicit approach manages large deformation problems with better success. So I switched my model to Abaqus/Explicit solver.
In explicit I tried two variants of time step:
(a) Total time of loading = 1 sec.
(b) Total time of loading = 10 sec.
The Amplitude was created in correspondence with this time.
I expected:
Bigger influence of inertia effects in the case (a), and so more reliable solution in the case (b)
I've got:
Big element distortions and "waves" in the case (b) and stable and fast solution on the case (a)
Could someone explain what is wrong? Maybe Explicit just can't solve problems with big times? Do you have any idea?
In attachment you can find a python script to create this problem on your machine.
Some pictures:
1. left picture: case(a), Time=0.55s; right picture: case(b), Time=5.5s
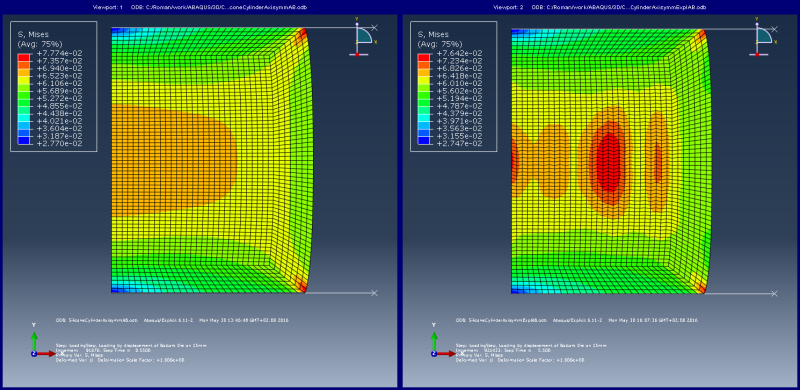
2. End of solution. left picture: case(a), Time=1.0s; right picture: case(b), Time=10s
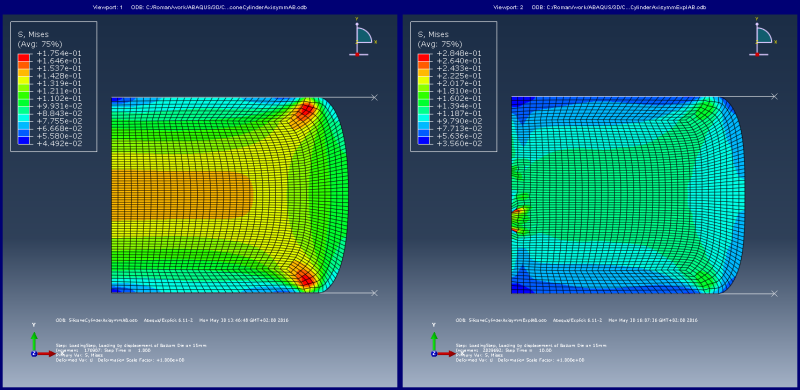
I wanted to make a very simple simulation - compression of cylindrical specimen. I was very surprised, when the solution was not converging.. and it is when more complex models work quiet well.
It is a second day, but still I didn't found completely the reason of this strange behaviour of my model.
Model:
Problem:
Cylinder (Arruda-Boyce hyperelastic model, height = 34 mm, diameter = 34 mm) is compressed between two analytically rigid plates. Axisymmetrical approach is used to solve the problem.
Contact:
between plates and specimen - surface-to-surface contact, with friction coeficient=0.1. Normal behaviour "Hard" or "Exponential" (I tried both).
BC:
Bottom plate is fully fixed, Top plate is going down(displacement BC) in order to compress cylindrical specimen with total 15mm displacement.
Abaqus/Standard:
First of all I started with Abaqus/Standard - problem is static, material is rate independent. Approximately at the middle of a step (~7.5 mm) time increment starts to decrease dramatically and finally reaches the minimum limit. On my opinion, large deformations leads to problem in contact zone, and as a result to very small time increment.
Abaqus/Explicit:
It is well known that generally Explicit approach manages large deformation problems with better success. So I switched my model to Abaqus/Explicit solver.
In explicit I tried two variants of time step:
(a) Total time of loading = 1 sec.
(b) Total time of loading = 10 sec.
The Amplitude was created in correspondence with this time.
I expected:
Bigger influence of inertia effects in the case (a), and so more reliable solution in the case (b)
I've got:
Big element distortions and "waves" in the case (b) and stable and fast solution on the case (a)
Could someone explain what is wrong? Maybe Explicit just can't solve problems with big times? Do you have any idea?
In attachment you can find a python script to create this problem on your machine.
Some pictures:
1. left picture: case(a), Time=0.55s; right picture: case(b), Time=5.5s

2. End of solution. left picture: case(a), Time=1.0s; right picture: case(b), Time=10s

