Stress concentration of a 3-D ellipsoid

[mp87]

Hi everybody,

I am struggling to find an analytic solution for the stress concentration due to a 3-D ellipsoid.

This article from Sadowsky and Sternberg dating back to 1949 dealt with the problem, and I tried to reproduce the same trend with the aid of a symbolic computation tool.

There must be something wrong somewhere since the resulting Kt as a function of the two shape ratios is the following:

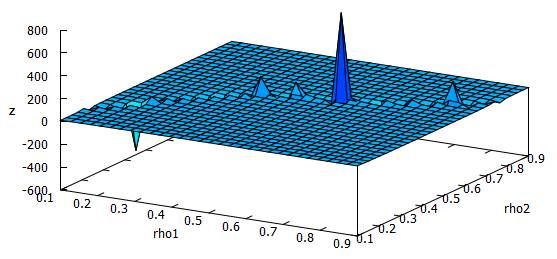
Is there someone who can lend a helping hand?

Many thanks.

Best regards,

Mattia

 

[Cockroach]

I have done this before, using elliptical relieves instead of standard rounded fillets in the corners of stepped shafts. Usually 3:1 ellipses give the lowest concentrations of stress, about 25% less or so.

Is this what you are trying to do? Finite element on the shaft is how I solved my uncertainty. You can get a decent estimate with advanced calculus involving elliptical integrals.

Regards,
Cockroach

 

[mp87]

Hi Cockroach,

Thanks for the interesting information.

My aim is a bit different, I want to carry out a stress analysis on an elliptic defect and I am therefore trying to derive the closed-form solution.
As you guessed, the calculation requires the use of elliptic integrals and Jacobi elliptic functions.
Are you familiar with it too?

 

[rb1957]

googling "stress concentration ellipsoid" got ...
on science direct ... "Stress concentration on an ellipsoidal inhomogeneity in an anisotropic elastic medium: PMM vol. 37, n≗2, 1973, pp. 306–315" (but you have to pay for it !)
and this gem ...

http://www.lajss.org/HistoricalArticles/Stress concentration around ellipitic hole.pdf

... free!

i'd've thought that Petersen would have covered it.


another day in paradise, or is paradise one day closer ?

 

[mp87]

... A Google search? Why didn't I think about it before?!?

Oh wait, I did Have a look at my first post and you'll find the same article you have linked. I have checked the other article too but it wasn't really helpful.

By the way, this case is included, although only in part, in Peterson's handbook (at least in its latest edition). How do I know it? Well, it's the second result coming out from a Google search with the keywords you have wisely suggested

 

[rb1957]

great, but you'd be surprised (or perhaps not) about how often people don't do the easy stuff.

I looked at the lajss document ... imposingly mathematical !

you need more than Petersen (3rd Ed) has ? his charts aren't enough ? his references ??

another day in paradise, or is paradise one day closer ?

 

[mp87]

That's curious, in my experience lazy people tend to start and finish their work on the same Google page (aka "The best place to hide a dead body is page 2 of Google search results" )

Yes the article is really impressive, especially considering the limited calculation tools available at that time. That's why I am feeling so disappointed by not being able to solve it.

Peterson gives just a general overview of the problem, and addresses the interested reader to the articles of Sadowsky and Sternberg for further details, including the one available on LAJSS website.
Unfortunately their works were published between the late '40s and '50s, while ASME Digital Collection does not provide articles older than 1960. So, I have no clue how I could find them.

 

[rb1957]

I guess it's a sign of the times that a google search is more than the minimum effort !?

I'm trying to understand your original pic ... if the z axis is showing stress at a (x,y) point on the ellipsoid surface, why isn't it a smooth surface ?

another day in paradise, or is paradise one day closer ?

 

[mp87]

I have purposely kept a certain ambiguity on the graph to arouse interest... The z axis represents the stress concentration factor Kt, while rho1 and rho2 are two shape factors thus defined: rho1 = b/a, rho2 = c/b, where a, b, and c are the three semi-axes of the ellipsoid.

 

[rb1957]

that's what I thought, but why the spikes in z ? (i'd've thought it'd've been a nice smooth curved surface)

another day in paradise, or is paradise one day closer ?

 

[mp87]

We cannot be 100% sure a priori that it will be smooth, but it cannot be negative as it appears to be now. So, I conclude that there is something wrong in the calculation. But the error is hidden somewhere in the mathematics, and I don't manage to figure out where and how to fix it.

 

[rb1957]

it's a smooth shape ... there'll be a smooth change in local stress. of all the possible shapes, the surface won't have large spikes (how I interpret your figure).

don't be so sure it won't be negative ... at a hole Kt = 3 on the loaded diameter, but -1 on the unloaded diameter; ie with 0deg and 180deg being across the hole along the tension stress, kt = 3, but at 90deg and 270deg kt = -1.

another day in paradise, or is paradise one day closer ?

 

[csk62]

@mp87

ASME transactions was the ASME journal before 1960, I believe. A few months back, I was looking endlessly for an ASME transactions article written in 1958, which as you state was not available on ASME digital collection. However, I did find out that these works are kept in print at the Linda Hall Engineering Library in Kansas City, Mo. If you know exactly what issue, year etc, they were very helpful in finding the article I requested, and then they scanned it and sent me a digital copy. I hope this helps you find your Sadowsky and Sternberg information.

 

[mp87]

@rb1957

Smooth shape implying smooth change in local stress -> It makes sense!
Negative SCF -> That of the hole is a good example, but in this case the SCF is calculated always at the same point and therefore the direction of stress does not vary.

@csk62

Thanks for the really great news! I'll contact them and ask if they can send me the articles. I have seen that they are applying a fee and rightly so, hope that it won't require a check as in some cases it's the only payment method US libraries accept.