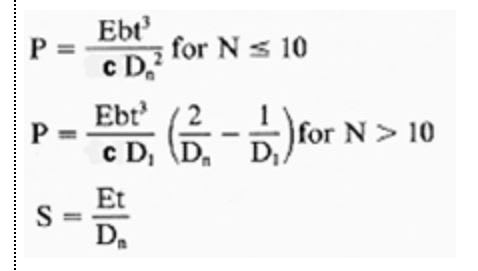Stress on strap wrapped around a drum 3

[random_guy]

Sometimes it's the easiest problems that give you the most trouble...

I'm estimating the fatigue life of a thin load carrying strap that's .008" thick and .75" wide, wrapped around a Ø0.1 m drum.

Fatigue from axial loading is as expected (10^9, not a high axial load).

For stress due to winding around the drum, I'm using the simple flexural stress equation: σ = E*c/ρ
You can't screw that calc up.

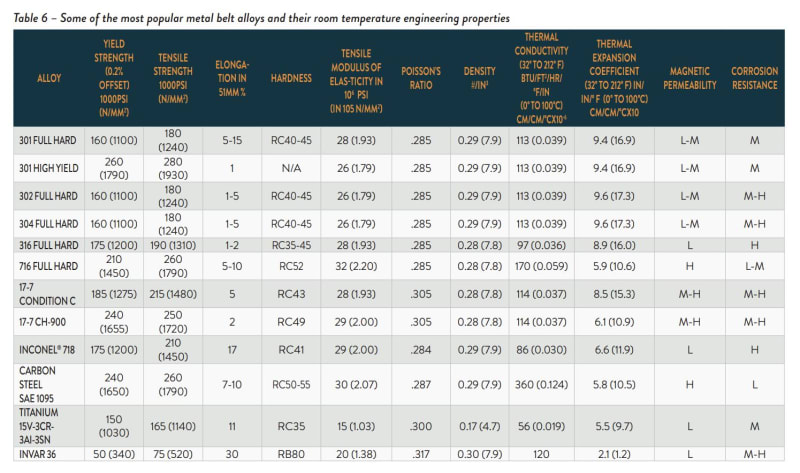
Stainless steel material. E = 193 GPa
c = 1/2t = 0.5*.008"*25.4/1000 = .0001016m
ρ = .05m

σ = E*c/ρ = (193e9 Pa)*(.0001016m)/.05m = 392 MPa

Sy is 207 GPa
Sut is 517 GPa

According to this calc, I'm nearly double Sy, well into the plastic range, and I should be seeing ~5500 cycles to failure.

Testing, however, has demonstrated around 100k cycles.

I'm at a loss as to where I've steered wrong. I even dug out an old strengths textbook and there's nearly an identical example with the same results.

Thoughts? Thanks in advance.



Wise men learn more from fools, than fools do from the wise.

 

[Snickster]

What I understand is that you are looking at the strap as a beam in flexure with compression on the inside (drum side) and tension on the outside. I believe a strap picking up a drum is not modeled as a beam in flexure but as a rope in tension that cannot support a moment. In this case each side of the strap supports half the weight of the of the drum putting the entire strap in tension equal to
=(weight/2)/Area Strap

 

[random_guy]

The drum is used to wind the strap to raise and lower the load attached at the other end.

But to your point, I agree that it seems this model is not the correct fit. However, numerous textbook examples demonstrate similar scenarios, including a steel cable around a drum (think overhead crane).

Ignoring the fatigue side of this, the resultant stress just seems much higher than it should be.

Wise men learn more from fools, than fools do from the wise.

 

[Snickster]

So the strap wraps around a drum with the loose end used to pick up something with a single strap crossection? Then the tension in the strap has to be weight picked up divided by area of the strap. As it wraps around the drum the friction of strap to drum reduces some of the tension.

 

[random_guy]

That would be the axial stress. And it won't be reduced, the load supported will always be held by the strap.

But there is a separate stress related to the bending of the material as it passes over the drum. That's where my discrepancy is.

Wise men learn more from fools, than fools do from the wise.

 

[Snickster]

Maybe so but I am not sure about that. I would need to think about it for a while. To me it is just like a rope using to lift something that is wound around a drum. There is only tension in the rope as a moment cannot be developed in it. If you apply any moment to it there will be no internal counter moment that can develop so only tension can exist. Maybe you can post the page from the book you are referring to that indicates a moment is developed.

 

[Snickster]

I can see though that there is a radius of curvature of a flat metal as it winds around the drum so possibly it could be that the inside that touches the drum is less stretched then the outside away from the drum that does produce some flexural resistance but with overall crossection still in tension. However to produce a resisting flexural moment a crossectional area must be able to resist shear. If you apply shear to a thin metal section or rope it will just deflect and cannot support shear.

 

[Snickster]

I see what you mean now. The radius of curvature is very small (2") and you therefore are in the plastic range even though it is a very thin piece of metal. So as you lift something you are going plastic as you wind up the load. But the load itself produces tension across the entire cross section, so I guess you are saying the load is not great enough to have any effect on the bending stresses due to curvature of the band around the drum (pipe). I don't think in metric units so I cannot get a feel for the magnitude of the load versus the bending but load must be great enough to produce the plastic bending around the drum in the first place. You sure you don't have a net positive tensile stress across the entire crossection? And what about friction of the band against the drum? Does this reduce the stress in the crossection. I am not up to crunching the numbers now - maybe tomorrow.

 

[Compositepro]

What is the drum dimeter? O.1 meter is not small in this case.

 

[Snickster]

4" is relatively small.

 

[GregLocock]

I agree with your calculation, and in order to bend it to that radius that bending moment must exist. So, definitely a puzzle.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[Compositepro]

0.008"/2" is 4 percent strain due to bending. Does that put you into plastic strain?

 

[MintJulep]

flexural stress equation: σ = E*c/ρ

The small drum and bend radius likely invalidates the beam curvature assumption that this formula is built on.

 

[MintJulep]

Try the constant force spring design equations.

https://www.engineersedge.com/spring_material/constant-force-spring.htm

Or, go all in and read this.

https://journals.sagepub.com/doi/10.1177/16878140211070450?icid=int.sj-full-text.similar-articles.2

 

[dvd]

p. 6 of attached literature from Sandvik Steel Conveyor Belt - Advice for Calculation and Design

 

[dvd]

p. 10 & 11 from DESIGN GUIDE AND ENGINEERS’ REFERENCE FOR METAL BELTS

 

[btrueblood]

The problem is most likely in your assumptions for strength of the strap material. 30 ksi is the typical yield strength for mild steel; your calculated stress is around 60 ksi. Lots of steels have yield stresses well above 60 ksi with only a small amount of alloy additions. Even if your strap is truly mild steel, its processing (cold rolling to achieve thickness would be one) could affect the true yield stress. Full hard (work hardened in the drawing process) spring wire can easily exceed 150 ksi yield strength.

Edit: your quoted material strengths are in GPa, I assume you meant MPa. 200 MPa is about 30 ksi.

 

[random_guy]

Thank you all for your input. This forum is amazing.

MintJulep - it's not a constant spring, but good idea. However, the equation referenced there is the same equation I was using.

dvd - These are excellent resources, thank you!
Interestingly, their equations use Poisson's ratio. When I crunch the numbers, I get a higher value of stress than using my first equation. They also list a helpful belt life expectancy based on pulley diameter to belt thickness, which for my scenario puts me around 800,000 cycles. They don't explain how they arrive at these numbers however.

I also notice that all of the materials they use in that guide have high tempers (full hard), giving large values for yield strength, which likely explains the high numbers for life expectancy.

So, I think I can conclude that my calculations are correct and the stresses from simply wrapping the strap around the drum are fairly high. However, this does not solve the question as to why I am greatly exceeding my estimated life. I think I need to take a harder look at my fatigue calcs.

Again - thank you all for your input!

Wise men learn more from fools, than fools do from the wise.

 

[random_guy]

btrueboold - you're absolutely correct. And my first suggestion was to utilize a stainless steel with a higher temper (I suggested 1/2 hard).

I was not assuming the strap material, it is annealed 302/304, and those values are accurate.

Wise men learn more from fools, than fools do from the wise.

 

[random_guy]

Although, I am looking at the material spec again, and the properties are listed as minimum yield and tensile strength.

I am now thinking that the actual values are much higher than that.

Wise men learn more from fools, than fools do from the wise.