albertoruenes
New member
Hi all,
I know this may sound like a very fundamental question, i just cant find an explanation in the literature.
R is defined as the ratio between the min and max stress, and depending its value has an impact on the fatigue test results by decreasing the stress amplitude as stress ratio decreases for the same number of life cycles.
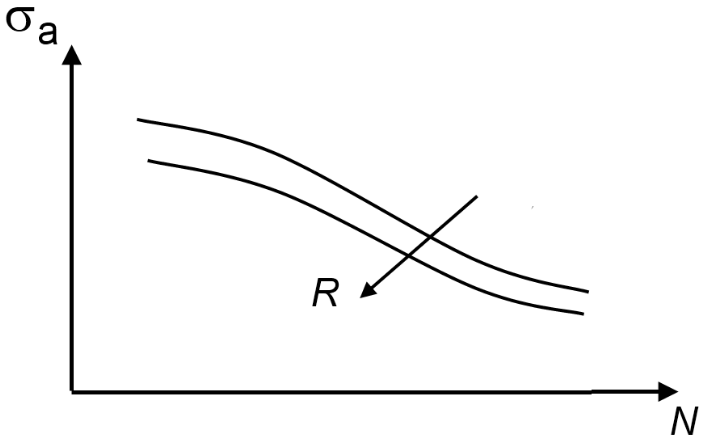
This R ratio is in direct relation with the mean stress and another graph states that as the mean stress becomes larger the stress amplitude will decrease. This makes total sense as the mean stress will have a greater contribution and actual life of the part will be affected, but i think that mathematically it contradicts the previous R ratio relationship, because as R ratio increases, mean stress also increase.
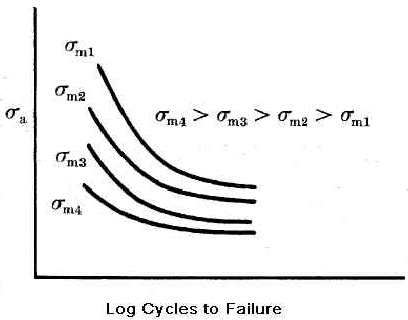
I know this might be very simple.
I appreciate all the help you can provide.
I know this may sound like a very fundamental question, i just cant find an explanation in the literature.
R is defined as the ratio between the min and max stress, and depending its value has an impact on the fatigue test results by decreasing the stress amplitude as stress ratio decreases for the same number of life cycles.

This R ratio is in direct relation with the mean stress and another graph states that as the mean stress becomes larger the stress amplitude will decrease. This makes total sense as the mean stress will have a greater contribution and actual life of the part will be affected, but i think that mathematically it contradicts the previous R ratio relationship, because as R ratio increases, mean stress also increase.

I know this might be very simple.
I appreciate all the help you can provide.
