Hello,
(sorry for reposting, I found later,this forum may be more appropriate).
This is a general micromechanic question.
Suppose we have a microstructured 2-phases material with random inclusions (or a porous material with random pores) and we make a real tensile test (monoaxial loading in the vertical direction of a specimen with nominal length L). We want to model such tensile test with FEM (for instance with Abaqus) like in this pic:

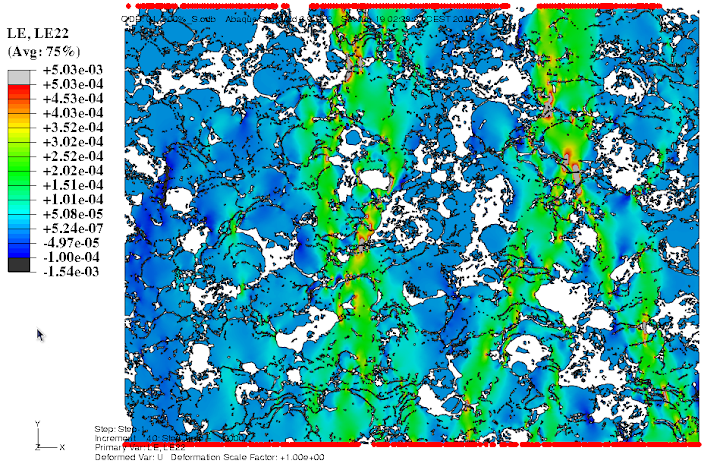
We can model the microstructure of the material, meshing a 2D subregion of the real specimen (like in the attached pic), so that the FEM solver can output a "strain field" across the 2D region at each time step of the simulation. Here an example [LE is the total log.strain~eng.strain for small elong. values]:
The experiment measures the strain as dL/L, where dL is the total elongation of the sample at the initial stress-free reference configuration.
The simulation makes the Bottom nodes of the model fixed in y and assigns to the TOP nodes a prescribed maximal strain (for instance 1%). Left and Right nodes can move (poisson effect) but parallel on the vertical axis.
I am now going to compare the experimental stress/strain with the calculated ones.
How to calculate correctly the "homogenized"(average) stress/strain to get a 1:1 comparison with the experiment?
I see two options:
A. the more intuitive one, I just take the simulated strain at the TOP boundary nodes of my model during all the step of the sim (the final one is the prescribed strain), because this seems to be what is actually measured by the experiment. The same for the Stress, since the force is trasmitted trought the TOP line of the model.
B. from the theory of micromechanics (seen in some scientific papers) we should actually average both stress and strain over the surface (volume).
Q: homogenizing stress by area is ok for me BUT for strain I have some doubts..: if a average strain over the area, than of course I underestimate the strain taken only from the TOP nodes (option A). This becasue I include in the average also those nodes closer to the fixed bottom part which have a lower strain.
What is the right way to calculate the average strain in order to compare it with experimental curves?
Thanks for help, Alex
(sorry for reposting, I found later,this forum may be more appropriate).
This is a general micromechanic question.
Suppose we have a microstructured 2-phases material with random inclusions (or a porous material with random pores) and we make a real tensile test (monoaxial loading in the vertical direction of a specimen with nominal length L). We want to model such tensile test with FEM (for instance with Abaqus) like in this pic:

We can model the microstructure of the material, meshing a 2D subregion of the real specimen (like in the attached pic), so that the FEM solver can output a "strain field" across the 2D region at each time step of the simulation. Here an example [LE is the total log.strain~eng.strain for small elong. values]:

The experiment measures the strain as dL/L, where dL is the total elongation of the sample at the initial stress-free reference configuration.
The simulation makes the Bottom nodes of the model fixed in y and assigns to the TOP nodes a prescribed maximal strain (for instance 1%). Left and Right nodes can move (poisson effect) but parallel on the vertical axis.
I am now going to compare the experimental stress/strain with the calculated ones.
How to calculate correctly the "homogenized"(average) stress/strain to get a 1:1 comparison with the experiment?
I see two options:
A. the more intuitive one, I just take the simulated strain at the TOP boundary nodes of my model during all the step of the sim (the final one is the prescribed strain), because this seems to be what is actually measured by the experiment. The same for the Stress, since the force is trasmitted trought the TOP line of the model.
B. from the theory of micromechanics (seen in some scientific papers) we should actually average both stress and strain over the surface (volume).
Q: homogenizing stress by area is ok for me BUT for strain I have some doubts..: if a average strain over the area, than of course I underestimate the strain taken only from the TOP nodes (option A). This becasue I include in the average also those nodes closer to the fixed bottom part which have a lower strain.
What is the right way to calculate the average strain in order to compare it with experimental curves?
Thanks for help, Alex
