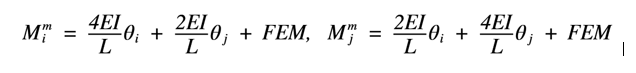Structure Design Using Slope-Deflection Equations and Matlab 1

[Tygra_1983]

Hi there, I was wondering if someone could help me.

I am designing a simple structure. I have attached a diagram and I am using the slope-deflection equations and using Matlab. Unfortunately I am getting strange results that I think are wrong. For the rotations at the joints I am getting zero which cannot be correct.

Here is my Matlab code:

clear
clc

% data

E = 2e+08;
I = 0.002;
EI = E.*I;
L1 = 5;
L2 = sqrt(5.^2 + 5.^2);
q = 100;
FEM1 = q.*L1.^2./12;
FEM2 = -FEM1;

% Symbolic mathematics

syms X1 X2 X3 X4 X5 X6 X7 X8 X9 X10

X1 = 0; X3 = 0; X5 = 0; X7 = 0;
X2 = -X8;
X4 = -X6;
X9 = -X10;

M1i = 4.*EI./L1.*X1 + 2.*EI./L1.*X2;
M1j = 2.*EI./L1.*X1 + 4.*EI./L1.*X2;

M2i = 4.*EI./L1.*X3 + 2.*EI./L1.*X4;
M2j = 2.*EI./L1.*X3 + 4.*EI./L1.*X4;

M3i = 4.*EI./L1.*X5 + 2.*EI./L1.*X6;
M3j = 2.*EI./L1.*X5 + 4.*EI./L1.*X6;

M4i = 4.*EI./L1.*X7 + 2.*EI./L1.*X8;
M4j = 2.*EI./L1.*X7 + 4.*EI./L1.*X8;

M5i = 4.*EI./L1.*X2 + 2.*EI./L1.*X4;
M5j = 2.*EI./L1.*X2 + 4.*EI./L1.*X4;

M6i = 4.*EI./L1.*X4 + 2.*EI./L1.*X6;
M6j = 2.*EI./L1.*X4 + 4.*EI./L1.*X6;

M7i = 4.*EI./L1.*X6 + 2.*EI./L1.*X8;
M7j = 2.*EI./L1.*X6 + 4.*EI./L1.*X8;

M8i = 4.*EI./L2.*X2 + 2.*EI./L2.*X9;
M8j = 2.*EI./L2.*X2 + 4.*EI./L2.*X9;

M9i = 4.*EI./L1.*X9 + 2.*EI./L1.*X10 + FEM1;
M9j = 2.*EI./L1.*X9 + 4.*EI./L1.*X10 + FEM2;

M10i = 4.*EI./L2.*X10 + 2.*EI./L2.*X8;
M10j = 2.*EI./L2.*X10 + 4.*EI./L2.*X8;

M11i = 4.*EI./L1.*X4 + 2.*EI./L1.*X9;
M11j = 2.*EI./L1.*X4 + 4.*EI./L1.*X9;

M12i = 4.*EI./L1.*X6 + 2.*EI./L1.*X10;
M12j = 2.*EI./L1.*X6 + 4.*EI./L1.*X10;

% Solving

Joint2 = M1j + M5i + M8i == 0

Joint4 = M2j + M5j + M11i + M6i == 0

Joint6 = M3i + M6j + M12i + M7i == 0

Joint8 = M4j + M7j + M10j == 0

Joint9 = M8j + M11j + M9i == 0

Joint10 = M9j + M10i + M12j == 0

Answer1 = solve(Joint2,X6)
Answer2 = solve(Joint4,X6)
Answer3 = solve(Joint6,X6)
Answer4 = solve(Joint8,X6)

solve(Answer1, Answer2)

I am hoping someone here knows how to use Matlab and is familiar with slope=deflection equations that can help me.

Kind regards

 

[GregLocock]

I haven't used solve for years but you have only initialised 4 of the Xs.

You need to list all the relevant Xs in each solve line, not just X6 , and I am fairly convinced your last line won't work.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[Tygra_1983]

Hi Greg, could you elaborate a bit more? Maybe could you copy and paste my Matlab code in yours and analyse it?

 

[Tygra_1983]

Is there any structural engineer here that can help?

 

[BAretired]

Well, I could possibly help with the structural part, but I am not familiar with Matlab, so I don't understand all of your equations.

Since the structure and the load are symmetrical, you could write slope-deflection equations for only half the joints. In your case, that would be joints 1, 2, 3, 4 and 9. Of course, if you load the structure unsymmetrically, you will need to write equations for every joint.

The slope deflection method, for any member spanning from A to B has two equations which are easily verified, namely:

M[sub]AB[/sub] = M[sub]FAB[/sub] + 2EI/L *(-2θ[sub]A[/sub] - θ[sub]B[/sub])

M[sub]BA[/sub] = M[sub]FBA[/sub] + 2EI/L *(-2θ[sub]B[/sub] - θ[sub]A[/sub])

EDIT: There are only three unknown rotations. They occur at nodes 2, 4 and 9 (rotation at nodes 1 and 3 is zero), so it should result in three simultaneous equations which should be soluble by hand methods. From that, the moments can be determined at all nodes.

BA

 

[BulbTheBuilder]

I go with BAretired. MATLAB is basically a matrix program, have them in a collective matrix and use inverse to find rotations. I also see "syms", did you use "eval" to evaluate those symbols? I haven't used MATLAB in a while so it could be I am missing something..

[Edit]-added these comments
1. MAB = MFAB + 2EI/L *(-2θA - θB);
2. MBA = MFBA + 2EI/L *(-2θB - θA);

Rewriting 1. MAB = MFAB - 4EI/L*θA -2EI/L*θB​

Rewriting 2. MBA = MFBA - 4EI/L*θB -2EI/L*θA​

Matrix becomes

[M] = [FEM - K][θ]​

MAB = [MFAB - 4EI/L - 2EI/L][θA]
MBA = [MFBA - 2EI/L - 4EI/L][θB]
since this expression is 'linear' use "\" not "inv" function. You can try "inv", I think that takes lots of computation time. Like I said, it has been a while I used MATLAb but I hope this helps

 

[BulbTheBuilder]

Alright, I think I see how you did yours, you used the "solve" function so it's basically the same concept. I would have to run your script and review the it later...let me know in the mean time if you find a fix or where the error was.

 

[Tygra_1983]

Hi NicOkai, thanks for your help. I still haven't figured what I am doing wrong. If you could do that, that would be great.

Have you gone through my slope-deflection equations at all? Because I'm not sure if the error is with my calculations or something to do with my Matlab code. I am using Matlab simply to reduce number crunching and make the calculations easier on myself. I downloaded the symbolic toolbox for Matlab so I could use symbolic mathematics.

Thanks again.

 

[Tygra_1983]

[URL unfurl="true"]https://res.cloudinary.com/engineering-com/image/upload/v1634124930/tips/Scan_structure_phoynf.pdf[/url]


Here is an updated attached diagram, so you can see how I have used Mi and Mj.

 

[Tygra_1983]

And I have used this format for my slope-deflection equations.

It Matlab I have replaced the theta1, theta2, theta3 etc... with X1, X2, X3 etc...

 

[BAretired]

The only difference I see is with the sign convention. In your formula, the theta values are positive when counterclockwise, but it shouldn't make any difference to the magnitude. For example, the FEM at Joint 9 is clockwise. With your equations, θ[sub]9[/sub] would be negative, but the magnitude would be the same.

BA

 

[BulbTheBuilder]

Hello Tygra, I got a little busy and couldn't run your script before. I will rub your script and go through but if you can, can you kindly try solving a simply-supported beam with the same script? Modify parameters to fit conditions and let's see the results we get.

[Edit]
Joint6 = M3i + M6j + M12i + M7i == 0 should be Joint6 = M3j + M6j + M12i + M7i == 0

 

[Tygra_1983]

Here, NicOkia

clear
clc
close all

L = 5;
q = 100
FEM1 = q.*L.^2./12;
EI = 400000;
FEM2 = -FEM1;

syms X1 X2


M1i = 4.*EI./L.*X1 + 2.*EI./L.*X2 + FEM1 == 0;
M1j = 2.*EI./L.*X1 + 4.*EI./L.*X2 + FEM2 == 0;

answer1 = solve(M1i,X1)
answer2 = solve(M1j,X1)

theta2 = solve(answer1)
theta1 = -theta2

PS: thanks BA retired for your help also!

 

[Tygra_1983]

Hi NicOkia,

Unfortunately, changing the equation using the j component still gives a result of X6,X8,X10 = 0. How have you found the code in your Matlab?

 

[BAretired]

@Tygra-1983

Try deleting the following lines from your code. The program should find all rotations without these lines.

X2 = -X8;
X4 = -X6;
X9 = -X10;

BA

 

[Tygra_1983]

Unfortunately, I'm still get the rotations to be zero BAretired! Even with that change.

 

[BulbTheBuilder]

Tygra,

Sorry, I failed to save the MATLAB file I was working on initially and was busy as well. I have a reminder set for me to go through your scripts again but I have scribbled something down to help us check. I would like you to make "E = 2e8", "I = 0.002", "L1 = 5", "L2 = sqrt(5.^2 + 5.^2)" as comments. Also instead of having FEM1 as an equation, just input 208.333. Run the script up to "Joint10 = M9j + M10i + M12j == 0".

I think the problem will come from "Answer1 = solve(Joint2,X6) Answer2 = solve(Joint4,X6) Answer3 = solve(Joint6,X6) Answer4 = solve(Joint8,X6)" so I want us to be sure. What I am seeing is, MATLAB is solving equation "Answer1 = solve(Joint2,X6)" for theta 6 but there's no theta 6 in Joint 2? For a system of equations, solutions are also dependent on other equations but I don;t see it in the MATLAB (from the way I see it). Lets say you have 3 unknowns and 3 equations, you need to solve them "simultaneously" but that's not done here. When you're done going through my attachment after making those changes I mentioned up there, try rewriting the system equations for the joints.

 

[Tygra_1983]

NicOkai, I think it is sorted. Firstly, I went straight ahead and changed Answer1 Answer2 etc... because that made a lot of sense. And now I have values that look correct.

I will paste the entire script and command window:

% data

E = 2e+08;
I = 0.002;
EI = E.*I;
L1 = 5;
L2 = sqrt(5.^2 + 5.^2);
q = 100;
FEM1 = q.*L1.^2./12;
FEM2 = -FEM1;

% Symbolic mathematics

syms X1 X2 X3 X4 X5 X6 X7 X8 X9 X10

X1 = 0; X3 = 0; X5 = 0; X7 = 0;


M1i = 4.*EI./L1.*X1 + 2.*EI./L1.*X2;
M1j = 2.*EI./L1.*X1 + 4.*EI./L1.*X2;

M2i = 4.*EI./L1.*X3 + 2.*EI./L1.*X4;
M2j = 2.*EI./L1.*X3 + 4.*EI./L1.*X4;

M3i = 4.*EI./L1.*X5 + 2.*EI./L1.*X6;
M3j = 2.*EI./L1.*X5 + 4.*EI./L1.*X6;

M4i = 4.*EI./L1.*X7 + 2.*EI./L1.*X8;
M4j = 2.*EI./L1.*X7 + 4.*EI./L1.*X8;

M5i = 4.*EI./L1.*X2 + 2.*EI./L1.*X4;
M5j = 2.*EI./L1.*X2 + 4.*EI./L1.*X4;

M6i = 4.*EI./L1.*X4 + 2.*EI./L1.*X6;
M6j = 2.*EI./L1.*X4 + 4.*EI./L1.*X6;

M7i = 4.*EI./L1.*X6 + 2.*EI./L1.*X8;
M7j = 2.*EI./L1.*X6 + 4.*EI./L1.*X8;

M8i = 4.*EI./L2.*X2 + 2.*EI./L2.*X9;
M8j = 2.*EI./L2.*X2 + 4.*EI./L2.*X9;

M9i = 4.*EI./L1.*X9 + 2.*EI./L1.*X10 + FEM1;
M9j = 2.*EI./L1.*X9 + 4.*EI./L1.*X10 + FEM2;

M10i = 4.*EI./L2.*X10 + 2.*EI./L2.*X8;
M10j = 2.*EI./L2.*X10 + 4.*EI./L2.*X8;

M11i = 4.*EI./L1.*X4 + 2.*EI./L1.*X9;
M11j = 2.*EI./L1.*X4 + 4.*EI./L1.*X9;

M12i = 4.*EI./L1.*X6 + 2.*EI./L1.*X10;
M12j = 2.*EI./L1.*X6 + 4.*EI./L1.*X10;

% Solving

Joint2 = vpa(M1j + M5i + M8i == 0,3)

Joint4 = vpa(M2j + M5j + M11i + M6i == 0,3)

Joint6 = vpa(M3j + M6j + M12i + M7i == 0,3)

Joint8 = vpa(M4j + M7j + M10j == 0,3)

Joint9 = vpa(M8j + M11j + M9i == 0,3)

Joint10 = vpa(M9j + M10i + M12j == 0,3)

Answer1 = vpa(solve(Joint2,X2),5)
Answer2 = vpa(solve(Joint4,X4),5)
Answer3 = vpa(solve(Joint6,X6),5)
Answer4 = vpa(solve(Joint8,X8),5)
Answer5 = vpa(solve(Joint9,X9),5)
Answer6 = vpa(solve(Joint10,X10),5)


theta = solve(Answer1, Answer2, Answer3, Answer4, Answer5, Answer6)

Command Window:

Joint2 =

8.66e+5*X2 + 1.6e+5*X4 + 1.13e+5*X9 == 0.0


Joint4 =

1.6e+5*X2 + 1.28e+6*X4 + 1.6e+5*X6 + 1.6e+5*X9 == 0.0


Joint6 =

1.6e+5*X4 + 1.28e+6*X6 + 1.6e+5*X8 + 1.6e+5*X10 == 0.0


Joint8 =

1.6e+5*X6 + 8.66e+5*X8 + 1.13e+5*X10 == 0.0


Joint9 =

1.13e+5*X2 + 1.6e+5*X4 + 8.66e+5*X9 + 1.6e+5*X10 + 208.0 == 0.0


Joint10 =

1.6e+5*X6 + 1.13e+5*X8 + 1.6e+5*X9 + 8.66e+5*X10 - 208.0 == 0.0


Answer1 =

- 0.1847*X4 - 0.1306*X9


Answer2 =

- 0.125*X2 - 0.125*X6 - 0.125*X9


Answer3 =

- 0.125*X4 - 0.125*X8 - 0.125*X10


Answer4 =

- 0.1847*X6 - 0.1306*X10


Answer5 =

- 0.1306*X2 - 0.1847*X4 - 0.1847*X10 - 0.00024049


Answer6 =

0.00024049 - 0.1306*X8 - 0.1847*X9 - 0.1847*X6


theta =

struct with fields:

X2: -0.00076274275732299026156747397808267
X4: -0.00031593839468454238506193227735856
X6: 0.00031593839468454238506193227735856
X8: 0.00076274275732299026156747397808267
X9: 0.00044680436263844787650554170072411
X10: -0.00044680436263844787650554170072411


What do you think??

Thanks so much for all your time an effort.

 

[BAretired]

Congratulations Tygra_1983! Perseverance paid off.

BA

 

[BulbTheBuilder]

That's good. You're getting results now. Let's validate those number now, plug them back in your joint equations and see if you get zeroes for the summation of moments. If yes, then you're good!