trying to work out an adjustable swiveling foot.
Would like to clamp a ball between two cones (would be threaded together) as illustrated. Known would be the contact angles (and thus the radii of the contact rings), the compression force along the common axis of the cones, and the friction coefficients. It would seem that the torque necessary to rotate the ball coaxially to the foot and the torque necessary to swivel off-axis would be different from each other -- how would I best calculate the latter?
Thanks in advance.
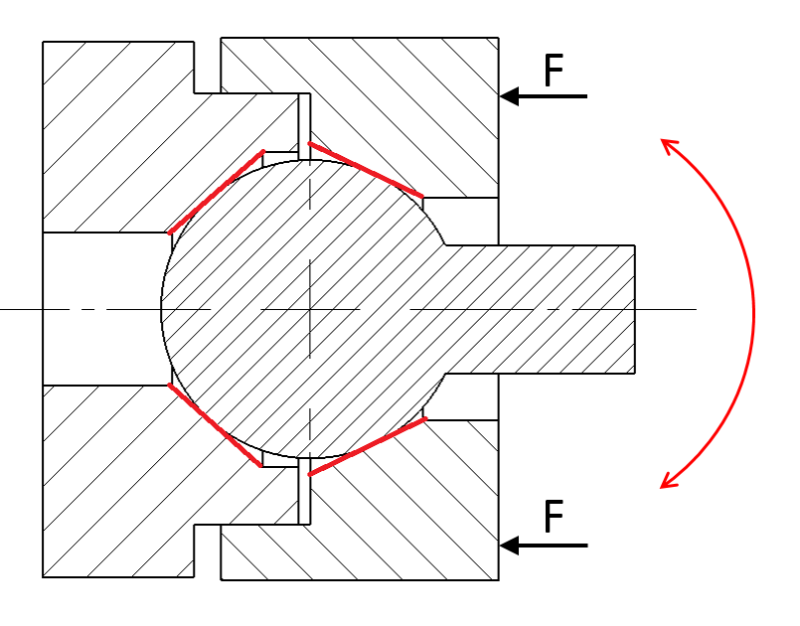
Would like to clamp a ball between two cones (would be threaded together) as illustrated. Known would be the contact angles (and thus the radii of the contact rings), the compression force along the common axis of the cones, and the friction coefficients. It would seem that the torque necessary to rotate the ball coaxially to the foot and the torque necessary to swivel off-axis would be different from each other -- how would I best calculate the latter?
Thanks in advance.

