eyemeyar
Structural
- Oct 16, 2014
- 14
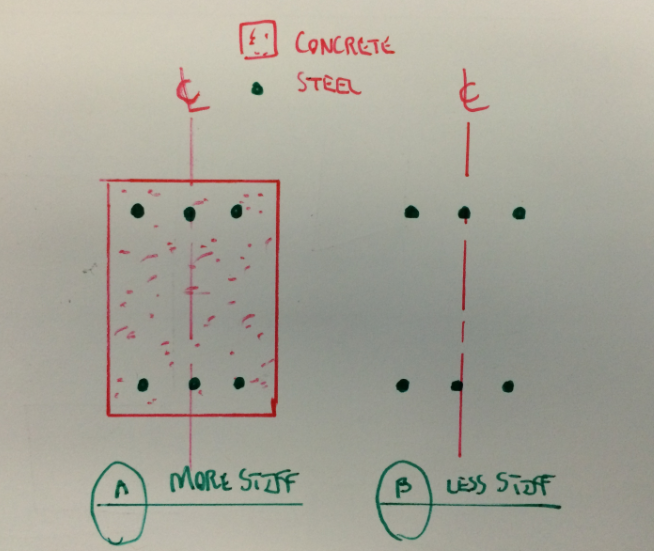
Hello Everyone. I would like to hear your ideas about doubly reinforced beams that has equal amount of reinforcement in compression and in tension. Is that ideal or no?
Thank you. =)
Thank you. =)
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
Of course we do. I was asking for some deatail and justification for your 2 x (ST stiffness w/o tension stiffening) shortcut as a reasonable upper bound estimate. Does it show up in print somewhere? Is there a graphical relationship that can be pointed to? Does it have a physical meaning that one might be find intuitive? Is it an extension of old school code recommendations like the 6X algorithm? Or do I just have to be smart enough to infer it from first principles somehow?
IDS said:but conservatively ignoring the concrete altogether can be accepted with no justification at all?
IDS said:Anyway, the justification is years of comparing results with more detailed calculations, and measured deflections (both research and on real projects).
IDS said:conservatively ignoring tension stiffening, and conservatively allowing for creep and shrinkage by multiplying by 2, needs detailed justification
IDS said:Approx Curve/ Best Estimate
Light Medium Heavy
IDS1 2.6 1.6 1.5
IDS2 2.2 1.4 1.3
Rapt 1.2 1.3 2.4
Kootk 3.0 1.6 1.3
rapt said:Kootk can rave on all he likes about more accurate methods that we expouse (not the 6* elastic gestimate), but they have shown to be relatively reliable in practice.
@IDS: any chance that seminar will be recorded or broadcast?
