Hello,
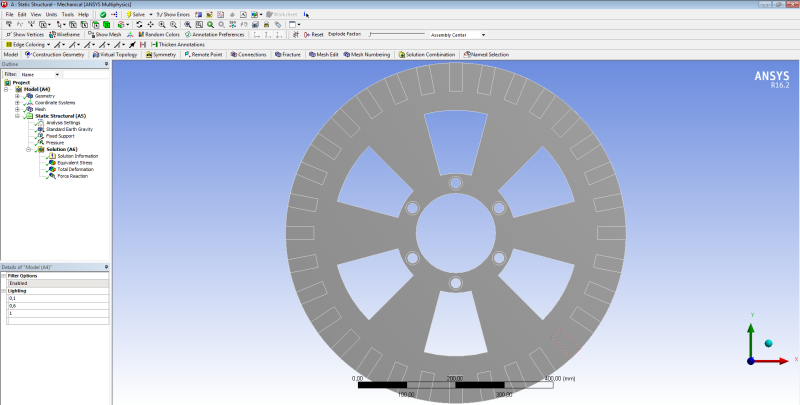
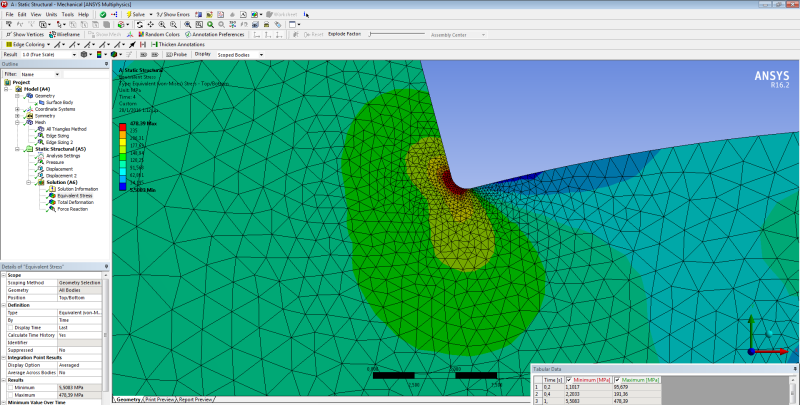
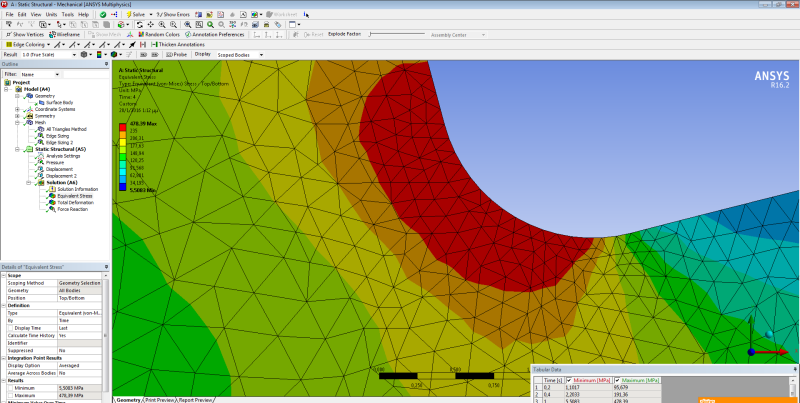
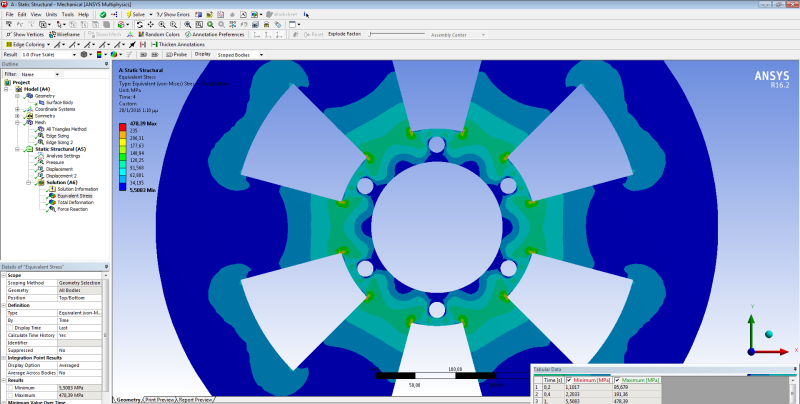
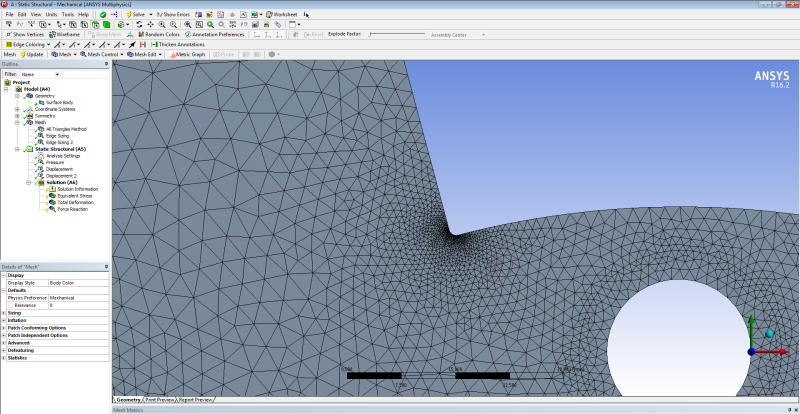
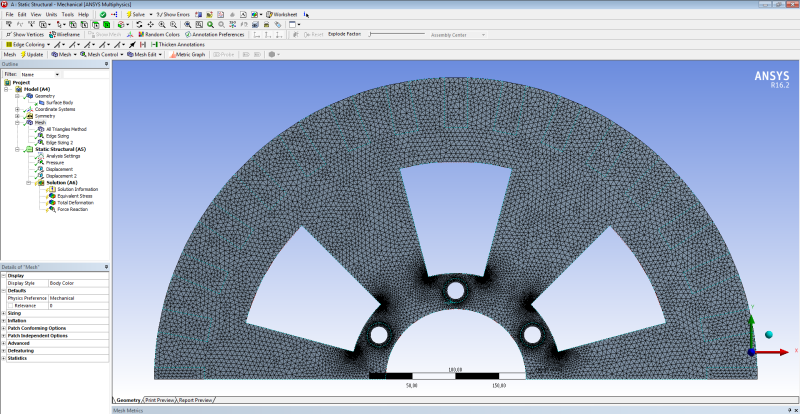
I use ANSYS Workbench for mechanical stress analysis of a thin metal circular disk (Diameter=700mm, Thickness=10mm) with some air gaps and a hole in the center (please see pics) subjected to bending. The results that I get for the equivalent von-Misses stress show me that in a very small region near the air gaps' corners the stresses are much larger than the yield strength( 235MPa) I tried to change the mesh (size and element type), and the boundary conditions but the results do not change significantly. The disk has been constructed and works properly with no sign of failure.
So the problem is: Is my model reliable? Is it possible the constructed disk to encounter such big stresses in such small regions without breaking? Can I trust the results of Ansys? Or there is something wrong I have done when I constructed the mesh..?
Sorry for the bad structure of the post, I am new to the forum..
Thank you in advance!
