Thin Steel Plate Arched Circle Design 1

[michmatt]

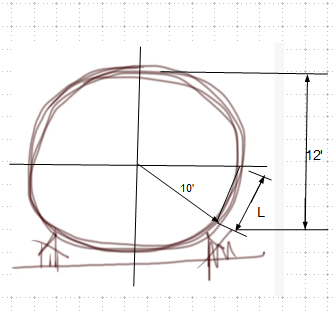
I am designing a structural steel art structure for exterior application. The structure is a relatively large steel circle (almost a full circle) anchored to a sub-surface concrete foundation. The architectural intent is to create a giant letter "O" with the base cut-off underground. The architect would like 500mm (20") wide x 20mm (3/4") thick steel plate. It will be powder-coated. The maximum span at the two extreme tangents is roughly 20 feet. The height is around 12 feet. It's not a perfect circle. The plate supports self-weight, snow, wind and other loads attributed to exterior art applications, but nothing very high. It is essentially a barrel arch with 500mm (20") length with a modified geometry that strays away from perfect arch geometry.

Can anyone suggest any good technical resources in guidelines or papers? AISC and ASCE have papers on stability and plate walls, but I don't think they apply here. A lot of shell/plate/membrane papers are for thicker concrete art structures which have their own nuances. I intend on analyzing with FEA for strength and serviceability, both in-plane and out-of-plane, but I would like additional focused information on global and local stability and other good tips. Slenderness checks are of importance here because there are areas of compression and tension, but effective lengths from codes and standards are likely not applicable to this type of structure. A detailed guideline or paper would be great.

Thank you.

M.

 

[MIStructE_IRE]

I dont have any guides... but don’t forget the weight of the skateboarders and the graffiti artist who climbs to the top!

Keep us posted though, it sounds very interesting!

20mm plate sounds very light for that diameter though. One kid up on top of it will buckle it instantly.

 

[WARose]

The trick to doing things like this is (as you have already guessed) stability. To that end there is Roark's and also 'Guide to Stability Design Criteria for Metal Structures' is another. For the latter reference, I've got the 3rd edition, and this (i.e. arches) is covered (for both in-plane and out of plane loads) on pp. 455-487.

 

[michmatt]

Thank you. I remember that textbook and I was searching for it online this morning with an incorrect title. My memory failed me, but I found it this afternoon with your help. Thanks again.

M.

 

[r13]

I think the wall thickness need to be checked against:

1) Excess deflection (global/localized).
2) Excess stress due to ring tension/compression.
3) Buckling of the lower leg (from tangent point of the circle to the support point). Euler critical buckling stress Pcr = π[sup]2[/sup]EI/L[sup]2[/sup] can be used.

I guess wind load will govern the design. Find a good reference, and be conservative.

 

[IDS]

3) Buckling of the lower leg (from tangent point of the circle to the support point). Euler critical buckling stress Pcr = π2EI/L2 can be used.

But what is L?

Be cautious using tabulated buckling solutions for arch structures subject to asymmetric loads.

I'd suggest doing a non-linear frame analysis using very short elements and including both material and geometric non-linearity, and check for a worst case live load, including impact.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[r13]

I think it wouldn't be too far off to use the chord length to start with. But I don't have any literature to back it up then.

 

[dold]

Didn't we have a similar discussion about the "goat spring board arch thing" a while back? [URL unfurl="true"]https://www.eng-tips.com/viewthread.cfm?qid=472867[/url] I wonder if you can glean any info from there?

 

[r13]

Do you really want people to walk through that lengthy thread to find the crown jewel?

 

[JStephen]

That sounds reasonably stout.
I think Roark has a load case with a circular ring loaded by its own weight and supported at one point. Your geometry and support details are somewhat different, but that load case would still be informative.
I believe there are also elastic buckling solutions for circular rings loaded in compression with buckling in the plane of the ring. There again, your geometry is different, but the results would be informative (and closer than trying to use a column approach).
In either case, if you deduce that a circular ring of similar dimensions is going to collapse under its own weight, or if you deduce that a circular ring of similar dimensions could support an elephant, it'll give you an idea what to expect from a more careful analysis.
A lot of the circular-ring analysis in the olden days was motivated by submarine design. Elliptical rings are a lot less common, but you might find some literature on them as well.

Sometimes, odd-shaped items like that can vibrate in the wind, and that would be hard to check without testing of some kind.

And it occurs to me, suppose some kid (or adult!) stands at one side and rhythmically pushes on the ring. How much would that make it move? Probably best not to build it in front of a middle school.

 

[michmatt]

Thank you everyone for your informative replies. I still haven't put pencil to paper on this one but I hope to chime back in with updates. We likely will have the steel fabricator build the full ring with the two bottom supports in their shop for verification. The geometry may change due to self-weight and it's better if the team accepts the droop in the shop. For loading yes we will include all of skateboarders, etc.

M.

 

[MIStructE_IRE]

Excuse my really bad sketch... done on the phone screen... But is this what we’re talking about?

 

[michmatt]

Yes.

 

[MIStructE_IRE]

r13 - in that case, what are you suggesting would be the “L” length for the Euler calc?

 

[r13]

The height is around 12 feet.

Assuming the chord length is 25", as a rough estimate, the thickness of the plate should be about 1", so it will yield prior to buckle.

 

[BAretired]

That looks like a really bad assumption, retired13.

BA

 

[r13]

BA,

Maybe. Don't forget, this is only the starting point, not the final.

The assumption is simple - the half circle is stable when subjected to in-plane stresses. However, the lower leg is critical, as the angle getting smaller, beam/column behavior is getting more pronounced, and the chord length is getting closer to the arch length. The application of Euler equation with pin-pin support is conservative, and the thickness, that would satisfy yielding prior to buckling, can be worked out. If the actual load is low, the thickness can be reduced, but the critical buckling stress needs to be re-checked. If the load requires a thicker plate, then buckling strength should be met.

 

[rb1957]

instead of a solid plate, how about two thin skins, say 0.25" thk, with 0.5" core between (so it looks solid) ?

another day in paradise, or is paradise one day closer ?

 

[BAretired]

BA,

Maybe. Don't forget, this is only the starting point, not the final.

It's not even a starting point. The chord length to be considered should be closer to the distance between a support and the top of the circle.


BA

 

[r13]

rb,

What is the core made of? Foam? Sounds a good idea.