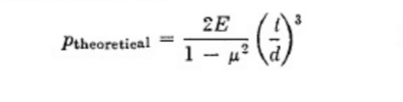Alatza
Mechanical
- Jun 26, 2016
- 8
Hello everyone!
I am designing a glass vacuum chamber to work with 0.001 Pa for a sputter coater.
The method I found is Von Mises equation for thin-walled cylinder buckling. More precisely, I am following this paper:
"Prediction of vacuum-induced buckling pressures of thin-walled cylinders".
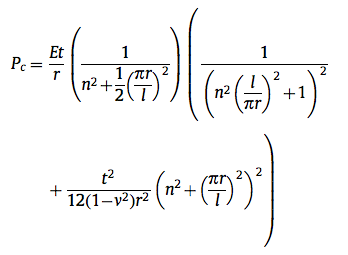
My parameters are:
E = 7.00E+10 Young's modulus for glass (Pa or N/m)
u = 0.2 Poisson's ratio for glass
r = 0.15 Inner radius (m)
t = 1.00E-03 Thickness (m)
l = 0.5 Length (m)
n = 6
Outside pressure= 1.01E+05 Pa (1 atm)
Inside pressure = 1.00E-03 Pa
Dif. pressure = 1.01E+05 Pa
The solution I found is: Critical pressure = 1.24E+07 Pa
This does not make sense since a glass only 1mm thick should not be able to handle all this pressure. Especially a piece so large.
I need to find the correct glass thickness.
Does anyone have a clue? What am I doing wrong?
Any help will be highly appreciated!
I am designing a glass vacuum chamber to work with 0.001 Pa for a sputter coater.
The method I found is Von Mises equation for thin-walled cylinder buckling. More precisely, I am following this paper:
"Prediction of vacuum-induced buckling pressures of thin-walled cylinders".
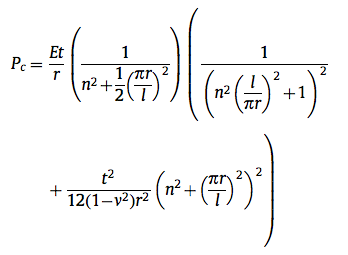
My parameters are:
E = 7.00E+10 Young's modulus for glass (Pa or N/m)
u = 0.2 Poisson's ratio for glass
r = 0.15 Inner radius (m)
t = 1.00E-03 Thickness (m)
l = 0.5 Length (m)
n = 6
Outside pressure= 1.01E+05 Pa (1 atm)
Inside pressure = 1.00E-03 Pa
Dif. pressure = 1.01E+05 Pa
The solution I found is: Critical pressure = 1.24E+07 Pa
This does not make sense since a glass only 1mm thick should not be able to handle all this pressure. Especially a piece so large.
I need to find the correct glass thickness.
Does anyone have a clue? What am I doing wrong?
Any help will be highly appreciated!