dp-17
Structural
- Jan 10, 2023
- 3
I am trying to model a tunnel as a three-hinged arch and I want to find out the bending moments (and shear forces) associated with a three hinge arch with a uniform distributed load on the top. See the below picture.
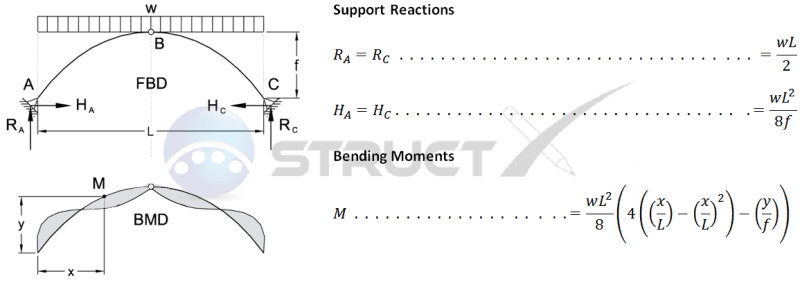
How can I calculate the bending moments? I have used the formula in the picture but I can't get the correct bending moment diagram that it shows in the photo. What am I doing wrong?

How can I calculate the bending moments? I have used the formula in the picture but I can't get the correct bending moment diagram that it shows in the photo. What am I doing wrong?
