Time to Drain a Full Pipe 1

[asaldes]

Dear Team,

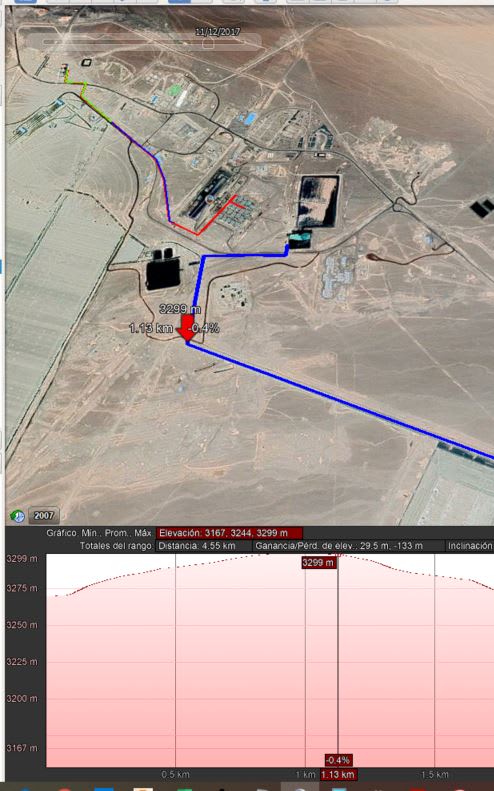
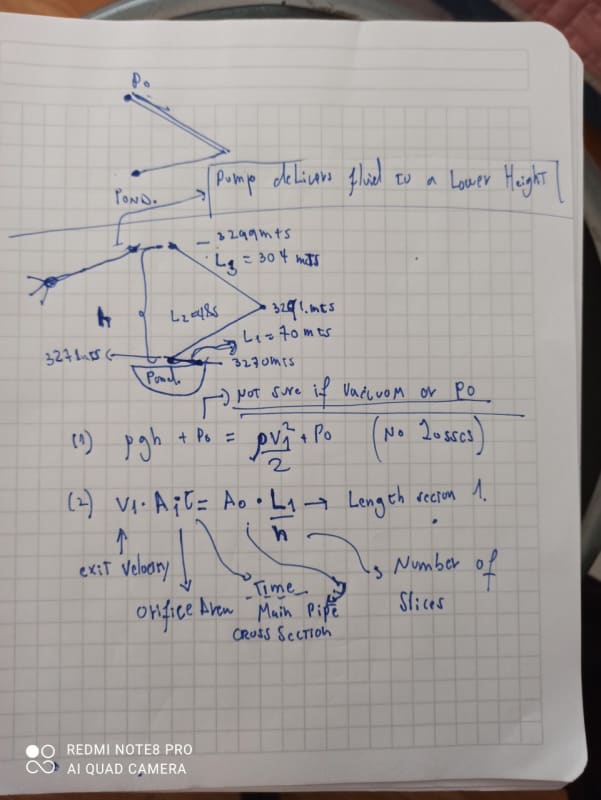
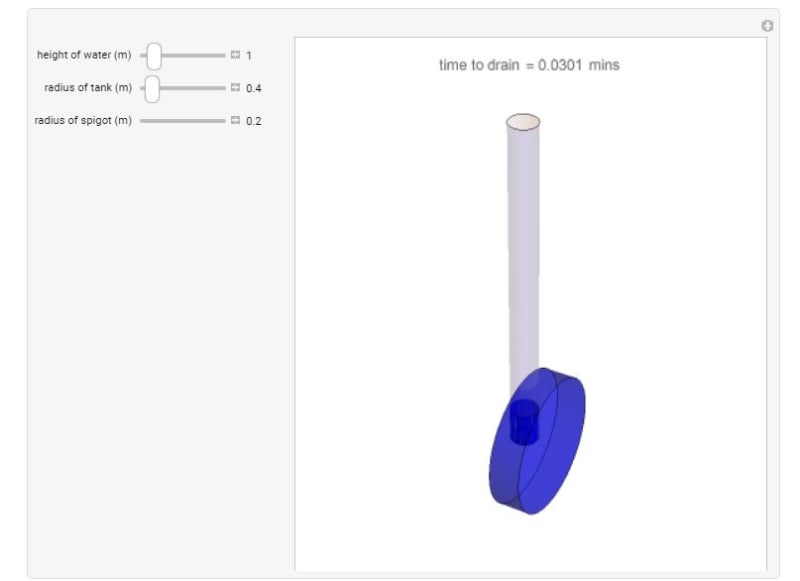
I need to calculate how much it takes to drain a 36" full pipe, in three main sections with different slopes. We have a 16" full open valve to drain it.


I do the calculation dividing the sections in several parts, estimate the velocity and then the volume flow trough the orifice. But this gave me a time of 11 minutes! i am not considering friction losses because I would need to estimate lambda in each part.

Can anybody give me a clue?

Best Regards to all the team

 

[LittleInch]

A slope drawing would help as would length.

Dressing can take a long tone as you have only a small pressure to drive the fluid out.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[Gator]

This post made me wonder about draining piping by pressurizing at a high point with an air pump or compressor. Is this ever done?

 

[LittleInch]

Yes, it is done and increases the flow.

The issue though and why you need to be VERY careful is how you cope with the air flow when you get to the end.

At some point you start to get blow by and get a lot of air with your water at high velocity as the air or gas vents.

If you're draining into a tank you can over pressure the tank very easily or end up with water spray out the end of your pipe.
Clearing a pipeline into an atmospheric storage tank went horribly wrong in one occasion and lifted the tank by several cm's. Only do it into an open top tank.

It's even worse if you're emptying it into a bucket.....

So you normally can't do it for volatile substances / chemicals as you create a large flammable or toxic vapour cloud.

The OP so far has told us about 10% of the information needed to help him or her, so difficult to go much further. IMHO.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[asaldes]

Thanks you for your reply. the system delivers water to an open pond. I uploaded two pictures, one with an image of the system and another with the different heigts. When the pumps stops, i assume that leaves a full pipe from the end of the line (3299 meters above sea level) and delivers it to the pond, at 3270 above the sea level. I´m not sure if I should consider that the fluid at 3299 mts is at atmospheric pressure, because that gaves me a too short time, if I assume vaccuom, that gaves when the flow is at 7 meters height a zero velocity.

Thanks you very much for your support.

 

[asaldes]

These are the equation i'm resolving:

Best regards

 

[1503-44]

I would try to consider the pipe as a tank lying on a slope and calculate the drain time similar to this, which is a method to calculate the time to gravity drain a vertical tank.

http://www.demonstrations.wolfram.com/TimeToDrainATankUsingTorricellisLaw

 

[asaldes]

Thanks you Five. What would be the tank height and base radius? If I use a tank i am not consider the slopes..

 

[1503-44]

Assume the "tank" is actually the pipe. Try the pipe diameter / 2 for the radius.
You need to slope the pipe-tank to get the correct height from discharge elevation to liquid level elevation.
Head, or Height = pipe_length * sin(slope_radians)

And remember, if you use atmospheric pressure at that elevation, it will be approximately 1/2 bars absolute.

 

[asaldes]

Thanks you Five for your answers again. but if I consider by example,the first section

I would have:

H (height Difference)=1 m= L sin(slope).
Tank Radius: Big pipe diameter/2.
Total Tank Volume=1 mtrs*tank radius^2*pi()=0.65 m3.

but the total volume that i need to remove (assuming full pipe) in this section is:

Total Volume= Pipe length*pipe radius^2*pi=45m3.

So I don't know if using the simulation and assuming a tank tool would give good results.

 

[1503-44]

I think it gives good results. The results are not convenient. You will not be able to drain that with only 1m head difference.
You need to pump it out with water pumped in behind pigs, or compressed air or nitrogen behind pigs, or it will take a very long time.

 

[asaldes]

That assumption gives a too small time!

regards, and again, thanks for your help

 

[1503-44]

Yes it is impossible to drain that in less than a ... week or two? Needs more head.

 

[asaldes]

So i'm not sure if I understand, Is the system only capable of remove 0.65 m3. of a total volume of 45m3??

 

[1503-44]

No that can be the flow rate from a long pipe, not a volume. Imagime that your pipe is connected to that tank. It takes 0.03 minutes (1.8sec) to drain a tank with a radius of 0.4m filled with 1m of water. That volume in the tank is 0.5 m3. So if you keep the tank at 1m of water by filling from your pipe, you will be emptying about 1m3 for every 3.6 sec. 2m3 in 7.2 seconds, 3m3 in 9 seconds. etc.

 

[LittleInch]

OK,

First things.

Do you know that the pipe is full when pumping? This makes a big difference to what is happening when the pump stops.
So first you need to define and make sure of the start conditions of the pipe when the pump stops before it is worth doing anything.

If there is no air vent but an open drain at the end then this line will pull a vacuum at the high point.

The friction losses in the pipe cannot be ignored over 800m. At 16" there will be some resistance ot flow but not too much I think.

Until the last 70m you seem to have a fairly steady slope.

So you have a head pressure of 29m minus lets say 5m for the vacuum at that altitude so 24m in 800m or 3m/100m of pipe.

For a 32" line this gives you a flowrate of about 9,000m3/hr or about 4.8m/sec. so that would be about 2 minutes.

Now that's moving so I currently don't think your pipe is running full uness you've got a back pressure valve on it. Do you?

HOWEVER your last 70m is only an elevation difference of 1m. This will take a long time to drain completly and will go into open channel flow.

Also as the head of water gets less than 5m, air will start to enter the pipe and start to go in reverse creating a glugging two phase flow ( a bit like emptying a bottle of water vertically). So throw all the calculations out of the window at that point.

If you really really want to find out, you need a transient simulation tool.

But why do you want to know? As opposed to just timing it with a watch?



Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[cvg]

first of all, you should avoid a vacuum unless you wish to collapse the pipe. secondly, it appears you are draining the entire thing through a 16 inch orifice with varying head pressure. the slope is not relevant since it appears that the flow is controlled through the orifice. until the very end, the pipe is basically full, and flowing under pressure equal to the height of water above the outlet. friction losses can also be ignored since the flow velocity will be quite low through the pipe. you will need to integrate the orifice flow which constantly changes due to the changing height of the water column.

 

[1503-44]

Asaldes, you need to clarify what your problem is about.

Are you "draining" this pipe after the pump stops, or are you pumping water all the time through this pipeline? I think you have confused everyone when you started talking about draining a pipe, then in the other post you started talking about pumps. I know now that I for one am confused.

 

[asaldes]

Sorry, Five, if my post wasn´t clear. I need to calculate the time to drain the pipe after the pump shut down., (normally the pumps deliver the fluid from the lower level to another level)after the 3299 mts heigth. To empty the pipe I assume full flow from the top until the 16 in full open valve

 

[1503-44]

OK then it sounds to me like you can estimate the outflow rate Q assuming it is a tank with a 1 meter of head.
So you have to check if the 16" diameter pipeline of length X meters and with Y meters of elevation change will sustain that same discharge flow rate Q.
In gravity powered systems (pumps off) liquids can flow at a rate where head lost to friction in the pipe equals the head gained from going down hill with the slope of the pipe.

The quick way to find the flow rate is to first find the head loss in a 16" diameter pipe with a flowrate of Q. The result will be something like H meters of head lost per L meters of pipe length. Now, if the actual slope of the pipe is less than that same H meters lost per L meters of pipe length, the pipe will not sustain the flow rate Q. It will flow at a lesser rate.
If the actual slope of the pipe is equal to H/L, then the pipe will flow at the same tank flow rate of Q. the level in the tank will decrease.
If the actual slope of the pipe is greater than H/L, the pipe will try to flow faster and the tank level will tend to increase which forces a new and higher discharge flow from the tank to result.
You can do a few iterations of that procedure to see how that goes.