Tolerance zone for true position of coaxial features 1

[Diametrix]

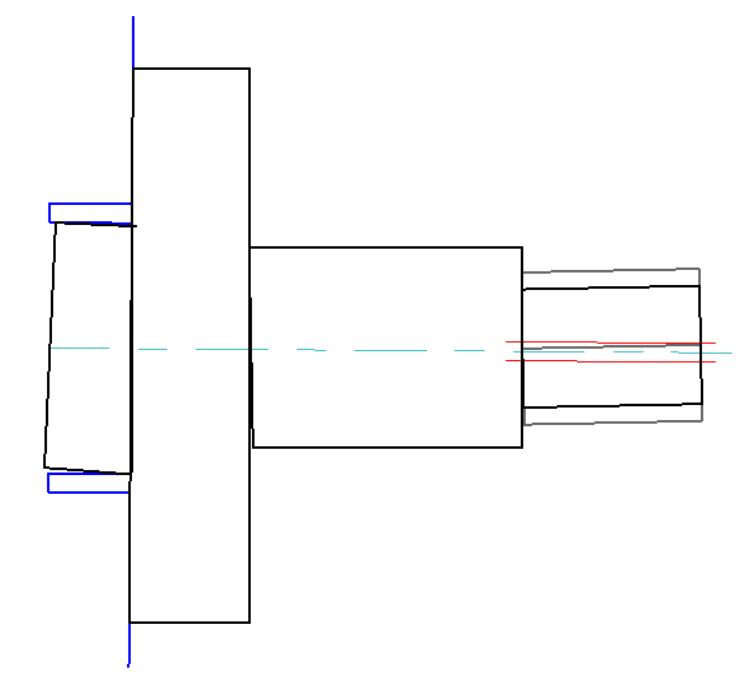
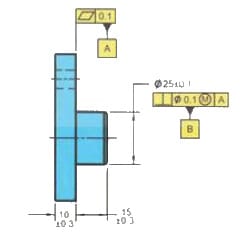
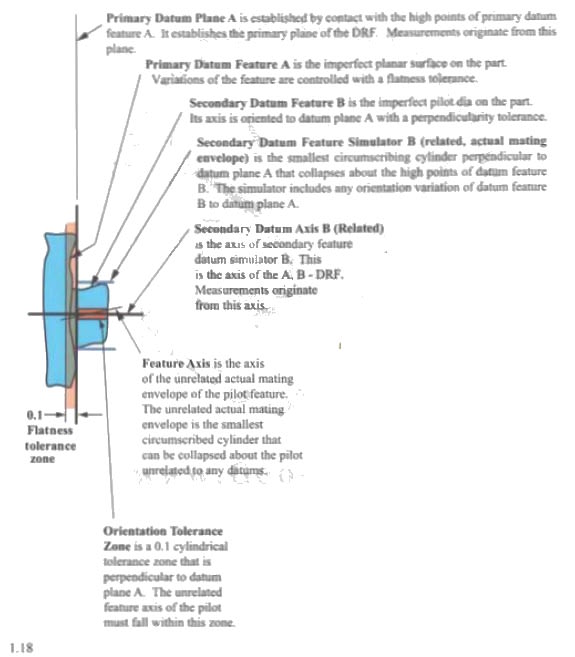
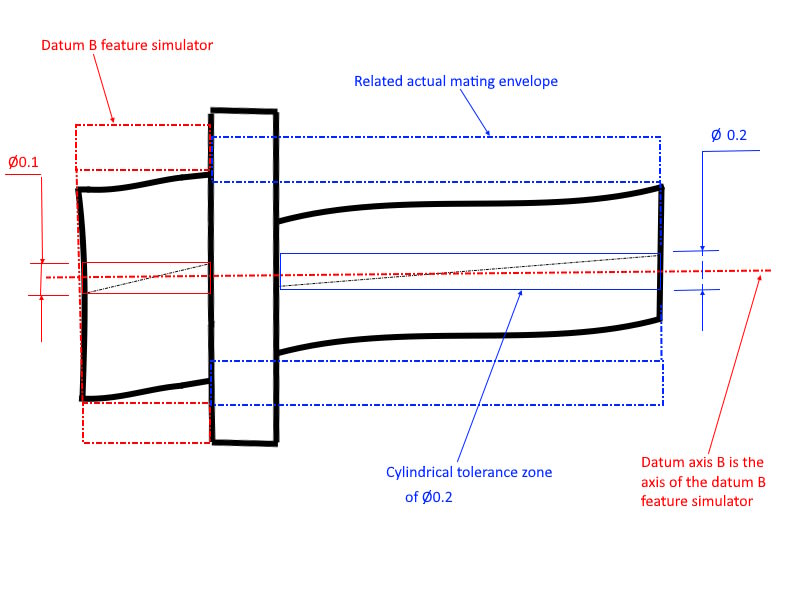
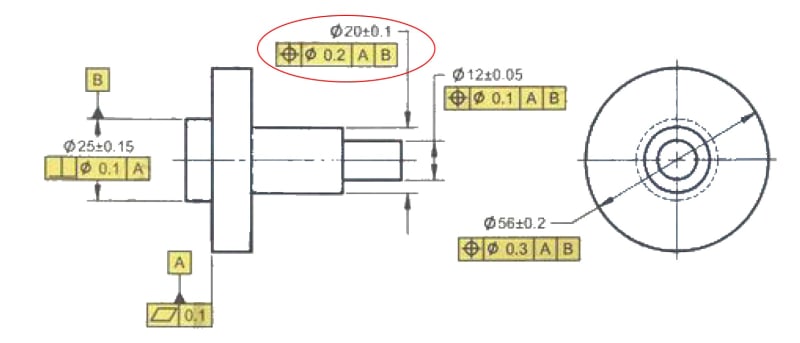
This came up on one of the drawings recently but I see it all the time, even in the textbooks. Say you have one circular feature with a perpendicularity constraint to a datum defined by a flat face and then you have another circular feature coaxial with the first one and having true position defined for it. For example Ø20 below

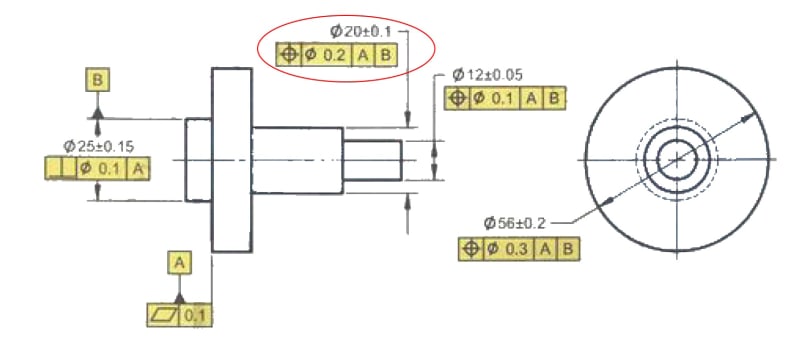
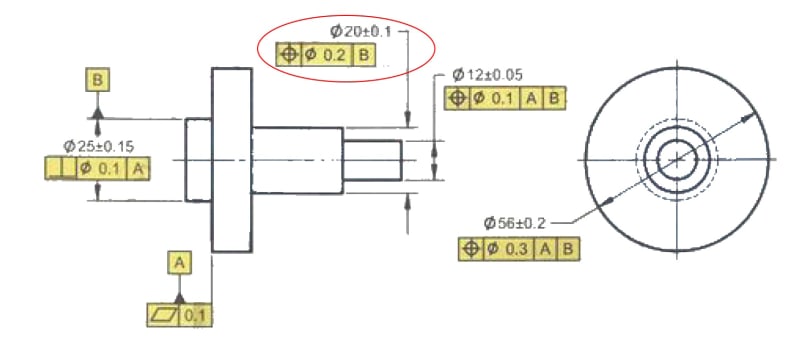
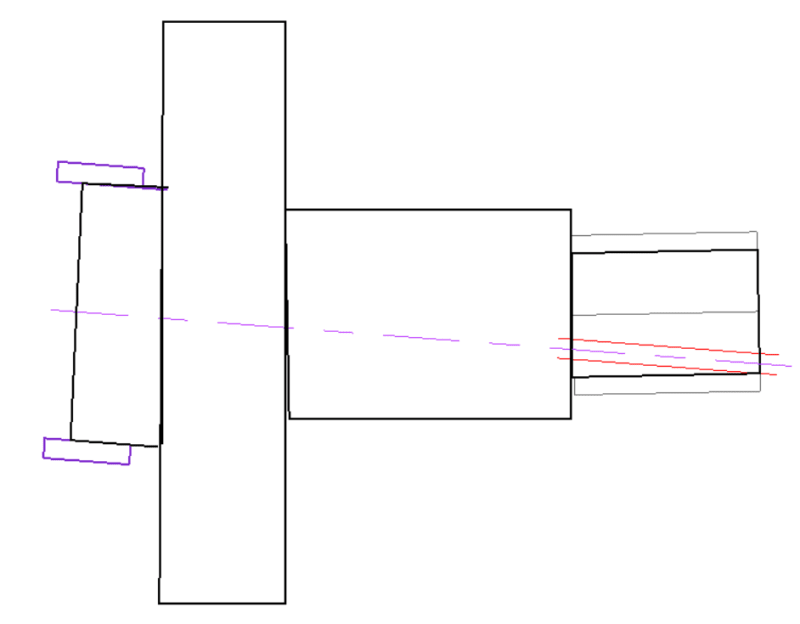
It is using two datums and establishes coaxiality to datum B and perpendicularity to datum A. My issue with that is that, the way I see it, using datum A doesn't add any additional constrain to the drawing. It defines exactly the same cylindrical tolerance zone around datum B axis, which is already perpendicular to the datum A. In other words, removing datum A from the feature control frame for that dimension will not affect the feature's tolerance zone at all... or am I missing something?

 

[Burunduk]

Referencing |A|B| or |B| is different and will result in two different inspection set-ups and different acceptable variations.
In the A, B scenario, the tolerance zone is centered to a datum axis (B) which is exactly perpendicular to datum A, which is derived from a datum feature simulator that makes full face contact with the actual datum feature A. Therefore the relationship between datum axis B and the actual datum feature B is not as tight as in the other case - the simulator of datum B is constrained to A and will not be the smallest cylinder that can contain datum feature B, but the smallest cylinder that can contain datum feature B AND remain exactly perpendicular to datum A.
If actual datum features A and B were perfect and exactly perpendicular, this wouldn't matter, but we know they can't be.

If the function of the part is such that datum feature A is forced to make full face contact with the mating part, then |A|B| represents the assembly conditions better than just |B| and it is preferable.

Hope this helps.

 

[greenimi]

It is using two datums and establishes coaxiality to datum B and perpendicularity to datum A. My issue with that is that, the way I see it, using datum A doesn't add any additional constrain to the drawing. It defines exactly the same cylindrical tolerance zone around datum B axis, which is already perpendicular to the datum A. In other words, removing datum A from the feature control frame for that dimension will not affect the feature's tolerance zone at all... or am I missing something?

Yes, You are missing a lot.
UAME (unrelated actual mating envelope) versus RAME (related actual mating envelope)
If you remove A then you have to orient the TZ to B only.

 

[Diametrix]

Thank you for your responses! Although, you did answer the questions I didn't ask... which was kind of the point I was trying to make. There is no doubt two cases have to be inspected differently and the setup for the case when you use both datums is going to be more involved. And the question at hand is: "Do both cases have the same TOLERANCE ZONE"

Let me illustrate:

Here is the case when both datums are used:

Here is the case when only Datum B is used

So, if the tolerance zone is the same in both cases you end up with a feature that has the same orientation and location constraints and it requires less effort to inspect it in the case when you specify only datum B

 

[Burunduk]

In the first case,
The axis of the evaluated feature has to be the axis of it's unrelated AME.

In the second case,
Datum axis B has to be the axis of the unrelated AME of the actual datum feature B.

Both cases are depicted wrong.

 

[axym]

Diametrix,

Burunduk and greenimi are both correct.

In the case where only Datum B is used, the B simulator needs to be aligned to the axis of datum feature B. In other words, simulator B needs to be the unrelated AME of B. Your drawing has it aligned perpendicular to A.

Evan Janeshewski

Axymetrix Quality Engineering Inc.

http://www.axymetrix.ca

 

[greenimi]

I think only Burunduk is correct. I am not.

"In the first case,
The axis of the evaluated feature has to be the axis of it's unrelated AME.

In the second case,
Datum axis B has to be the axis of the unrelated AME of the actual datum feature B."


See this discussion and the sketch from Tec-Ease

https://www.eng-tips.com/viewthread.cfm?qid=423773

 

[Diametrix]

That's still not an answer to the question. But ok, let's discuss the basics.

In the first case,
The axis of the evaluated feature has to be the axis of it's unrelated AME.

The first case is the case of Ø0.2|A|B Why would it be unrelated if there is a perpendicularity constraint to datum A?

In the second case,
Datum axis B has to be the axis of the unrelated AME of the actual datum feature B.

Datum axis B doesn't change from case to case. It stays the same and is defined by related AME which is defined by perpendicularity tolerance to datum A.

In the case where only Datum B is used, the B simulator needs to be aligned to the axis of datum feature B. In other words, simulator B needs to be the unrelated AME of B. Your drawing has it aligned perpendicular to A.

You guys making me doubt my sanity. Again, Datum B doesn't change from one example to the next and it remains perpendicular to datum A. May be I didn't explain this well enough Here are the two examples I'm talking about:

Example one as above:

Example two (feature with the Ø20 references only datum B):

That aside, everybody keeps getting hung up on the details without addressing the original question

 

[Diametrix]

If you remove A then you have to orient the TZ to B only.

Axis of the datum B simulator is already perpendicular to datum A. So there would not be any change in the tolerance zone orientation.

 

[greenimi]

Axis of the datum B simulator is already perpendicular to datum A.

I don't think that if B is primary in the positional callout, the requirement of B simulator to be perpendicular to A is a valid one. Therefore, again, not the case.

 

[axym]

Diametrix,

I'll try to address the original question. The tolerance zone is the same - it's a 0.2 diameter cylinder that is coaxial with datum axis B. What changes is the actual part's relationship to datum axis B, and hence the toleranced feature's relationship with the tolerance zone.

We're getting hung up on the details because the details are important. However, it can be difficult to get the point across in words - pictures are usually necessary. Your diagrams are great, but they show that there are a couple of details that you're not seeing correctly. Here is what it should look like when only datum B is referenced:

If we look at this, Burunduk's and greenimi's statements should make sense. Hope that helps.

I just noticed that I sketched the zone for a different feature. But the same thing applies.

Evan Janeshewski

Axymetrix Quality Engineering Inc.

http://www.axymetrix.ca

 

[Burunduk]

But ok, let's discuss the basics

Good idea. The basics is what you should focus on, for now.

The first case is the case of Ø0.2|A|B Why would it be unrelated if there is a perpendicularity constraint to datum A

The axis being evaluated within the position tolerance zone is ALWAYS the axis of the unrelated actual mating envelope of the considered feature. The perpendicularity constraint is for the simulator of datum B.

Datum axis B doesn't change from case to case. It stays the same and is defined by related AME which is defined by perpendicularity tolerance to datum A.

Datum axis B is the axis of the unrelated AME if only datum feature B is referenced, and it is the axis of the related AME (perpendicular to datum A) if datum features A primary, B secondary are referenced.

Again, Datum B doesn't change from one example to the next, and it remains perpendicular to datum A.

Again, it is perpendicular to datum A only when datum feature B is referenced secondary after A. If B is the only one referenced, it is considered primary and the datum axis is the axis of the smallest cylinder that circumscribes datum feature B without any constraints (the unrelated actual mating envelope).

Regarding the tolerance zone:
You got one thing right, the tolerance zone is always centered to datum axis B.
But as Evan pointed out, the orientation of the PART changes relative to the datum axis and the tolerance zone from case to case. I attempted to explain that in my first response in this thread. So if you paid attention, this actually could be the answer to your main question.

Check Evan's illustration. It captures the meaning of the |B| case quite well.

 

[axym]

All,

FWIW, here's the alignment for the A|B reference on the same as-produced part geometry.

This time, datum axis B is derived from a related AME (that is exactly perpendicular to datum plane A). The axis for the feature controlled by the position tolerance is the unrelated AME.

Evan Janeshewski

Axymetrix Quality Engineering Inc.

http://www.axymetrix.ca

 

[Diametrix]

Well, it seems my understanding of GD&T is severely lacking indeed. I guess that's why I'm here to learn something.

It seems to be the greatest disconnect that I have with yall explanation has to do with the datum B. So bear with me. You all pretty much agree that datum axis B is the axis of the unrelated AME. Why?

Here is one statement:

The axis being evaluated within the position tolerance zone is ALWAYS the axis of the unrelated actual mating envelope of the considered feature. The perpendicularity constraint is for the simulator of datum B

In other words, you are saying here that if I reference any cylindrical datum I reference feature mating envelope axis and not datum simulator axis?

Here is an example from a textbook that seems to contradict that statement:

Now datum feature in this example is not related to anything. It is just two coaxial features one of which is used as datum. The point I'm trying to make with this example that: "...cylindrical tolerance zone is concentric with datum axis" and "Datum axis A is the axis of the datum feature simulator" In this case Datum Feature simulator is defined by an unrelated actual mating envelope. But the distinction is important here. If we use the axis of datum feature simulator rather than an axis of the feature - those two will not always coincide. Now what would the axis of the Datum Feature Simulator would look like if the datum feature had a perpendicularity constrain?

Here another example from a textbook:

The main thing here is that feature axis and Datum axis are not the same. And datum axis is perpendicular to the primary datum.

So if I put this two examples together then I would get the following: 1. When we use a datum letter in a feature control frame we reference that datum feature simulator axis (as apposed to the feature axis) 2. Datum feature simulator axis of a cylindrical feature with a perpendicularity constraint is an axis of related mating envelope.

So where did I go wrong here?

 

[3DDave]

The typical case is for the pilot diameter to be very, very short. So short that the direction of the axis is very difficult to determine.

So a planar surface is chosen to set the direction of the datum axis which is forced to be normal/perpendicular to that nominally planar surface and the center of the pilot diameter sets the location of the datum axis based on the "related actual mating envelope" of that pilot diameter.

Once the direction, perpendicular to the primary datum feature simulator plane, and location of the center of the datum feature simulator related actual mating envelope for the pilot diameter are known, the unrelated (which is a dumb term as the FCF tells there is a relation to a datum reference frame, but committees, right?) feature simulator axis of the toleranced feature has to lie within the tolerance zone surrounding the simulated datum axis.

 

[Burunduk]

In other words, you are saying here that if I reference any cylindrical datum I reference feature mating envelope axis and not datum simulator axis?

I don't. The main point of the quote you addressed by this question, is that the evaluated axis (of the controlled feature to which the position tolerance applies) is always the "feature axis", i.e. the axis of the "unrelated actual mating envelope" of the feature.
The constraints for the simulator of the datum axis (the "datum feature simulator") depend on the place of the cylindrical datum feature in the datum precedence order as it appears in the feature control frame.
For a primary datum feature (including the case of a single datum reference like in your first textbook example), the datum feature simulator is independent. It is simply the smallest cylinder that can include the datum feature. It is named appropriately, the "Unrelated AME".
For a secondary datum feature (like in your second textbook example), the datum feature simulator is no longer the smallest independent cylinder contracted about the cylindrical datum feature. It is now the smallest cylinder that can contain the datum feature AND be precisely perpendicular to datum plane A in the example (the plane that is tangent to datum feature A at least 3 high points).
Between the 2 cases, the part ends up oriented differently relative to the datum axis and the tolerance zone.

 

[axym]

Diametrix,

I agree with everything in Burunduk's latest post. A couple of further thoughts that may help:

The datum axis (that is, the relationship between the datum axis and the actual datum feature) depends on how that datum feature is referenced in the FCF. If the cylindrical datum feature is referenced as primary, it's the axis of the unrelated AME. If the cylindrical datum feature is referenced as secondary, it's the axis of a related AME (an AME that is oriented or located to the primary datum). So there can be a different datum axis B for different FCF's on the same drawing.

The presence of the perpendicularity tolerance of feature B relative to feature A does not directly influence the datum feature simulators or how they contact the datum feature(s). This is determined only by how the datum features referenced in a particular FCF. So if the datum feature reference is just B, then the perpendicularity to A (or anything else to do with A) doesn't affect the DRF.

There are figures in the Y14.5 standard that show the DRF's resulting from the same datum features being referenced in different sequences and with different modifiers. In 2009 it's 4-20 and 4-21, in 2018 it's 7-19 and 7-20.



Evan Janeshewski

Axymetrix Quality Engineering Inc.

http://www.axymetrix.ca

 

[Diametrix]

evaluated axis (of the controlled feature to which the position tolerance applies) is always the "feature axis"

No argument from me here
However right after the statement I quoted in the previous post you said:

Datum axis B is the axis of the unrelated AME if only datum feature B is referenced

Are you saying that datum axis B changes depending on the fact that some other feature references datum B or not? What if it is not referenced by any other feature at all? Datum B ceases to exist? That seems like putting the carriage before the horse. Second textbook example above shows that datum B axis is established regardless of any other feature referencing it.

 

[Diametrix]

In 2009 it's 4-20 and 4-21, in 2018 it's 7-19 and 7-20

Thank you for the references! If you don't mind I have one more followup question. What if the datum B is a secondary datum in the FCF, but primary is some other cylindrical datum, let's say C. Datum B is still perpendicular to the datum A (just like in the original example). So if I put Ø0.2|C|B does it mean that the axis of the related AME of the datum feature B will be used? I fail to understand the logic behind this arrangement.

 

[3DDave]

This is why I want simulation software to generate conforming models with variation. Failing to understand the logic after this many attempts from us and the standard, possibly, and the myriad of other available sources means that only a tool that allows immediate feedback as to the results expected will provide an understanding of the relation of those results to the requirements.

At the least that simulation software used with tolerance analysis software will show if the overall scheme will work in spite of not understanding the logic.