Torque Principles

[LL631]

Hello,

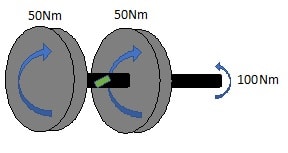
I am trying to assess the effect of inertia distribution on the reading from an In-line torque sensor in a small scale inertia dynamometer. As shown below the system has a rotary torque sensor with a brake attached to one end and an inertia mass on the other. The inertia is brought up to speed by the motor, the clutch decouples the motor, the brake is applied and the torque transducer measures the torque as the system is brought to rest. My head tells me that in this system the torque through the transducer(the measurement)is dependent on the distribution of inertia between the load-end & brake-end.

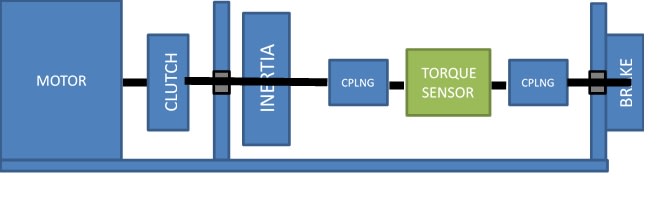
To simplify the system I treat all inertia on the load-end as one inertia mass (I2) & all inertia on the brake-end as another (I1), the shaft between the two represents the transducer. The transducer shaft and brake shaft have the same stiffness and 0 inertia. There is also no drag or play.

The brake torque causes the system (inertia) to decelerate: T_B = I X a.

The inertia resists deceleration therefor creates a reaction torque: T_B = T_Reaction

The total reaction is the sum of the individual parts: T_b= T₁+ T₂.

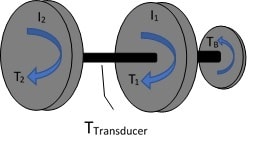
It is then obvious that the torque measured over the transducer is T_B - T₁.

Is this theory correct? I know the situation is very simplified, I just need enough proof to argue the point against using this equipment setup.

Cheers

 

[SwinnyGG]

I just need enough proof to argue the point against using this equipment setup.

Why, specifically, do you think this setup is not correct? The transducer, as located, will tell you how much torque is being applied to the inertia mass/coupling/shaft on that side.

What are you trying to accomplish?

 

[LL631]

I think this setup is incorrect because the reading of the transducer is dependent on the ratio of inertia at either end.

Imagine the transducer is a simple strain gauge. In one setup the strain gauge is placed on a spinning shaft with a large flywheel on one end, you then apply 100Nm to the other end to slow it down. The strain in the shaft will be equivalent to 100Nm.

Now cut the shaft in half and fix the flywheel between the two. Apply the torque to the end of the shaft without the strain gauge, leave the other end free. The strain in brake shaft will be equivalent to 100Nm but the strain in the shaft with the sensor will be almost nothing.

Now add a second identical inertia to the free end of the shaft with tne sensor and apply the torque again. This time the strain in the shaft with the sensor will be equivalent to half the torque produced by the brake.

This effect will take place in my system, albeit at a much reduced effect. For instance we may be asked to run a total system inertia of 0.002kgm^2, assuming the inertia on the active end is around 0.0002kgm^2 this would give a 10% error.

 

[LL631]

I am developing a small scale dynamometer for my company, I need understand the effects of such a setup so i can compare to other options.

An alternative is the brake fixture is mounted on bearings so is free to rotate. The fixture has a torque arm so can transfer the reaction torque from the brake to a force sensor - this way the entire inertia of the system is coupled to the sensor.

 

[SwinnyGG]

You're not wrong.. but the real question is, so what?

In the real world, it is impossible for the mass of the physical assembly on either side of your torque transducer to be zero. If you're characterizing brake torque (which is what it appears that you're doing) then the transducer must always be between the brake assembly and the test mass. There's no other place for it to go.

You solve the error by characterizing your machine- the mass of the shafting/coupler on each side of the torque transducer are very easy to measure and account for in your calculation of actual power dissipated by the brake.

 

[BrianE22]

At what point along the shaft do you want the torque measurement? Yes, it is true that the torque will vary along the shaft because of the lumped inertias. If you want the torque from the brake then your transducer needs to be mounted so that there is minimal inertia between the torque measuring device and the brake.

 

[desertfox]

Hi

Have a look at this site

https://appmeas.co.uk/products/torque-sensors/

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein