NorthCivil
Civil/Environmental
I've got a weird one that i know i could have solved in my university days, but has me scratching my head these days.
I have a column, fully fixed at both ends, very tall (~9metres)
It is subject to near nil compressive forces, or bending forces (no WL2/8 business). but it is very tall, ideally slender, and subject to a rotational load (from a big piece of signage which will me mounted off of the side, cantilevered out ~2 ft or so.)
the rotational force upon it will be quite large.
I am having trouble checking the column for rotational deflection. i have my old mechanics of materials textbooks out, but they are going deep into differential equations to solve, and don't have this particular case solved.
there must be some way to express/calculate the deflection in radians?
the idea is this sign shouldnt be flapping back and forth too much in the wind.
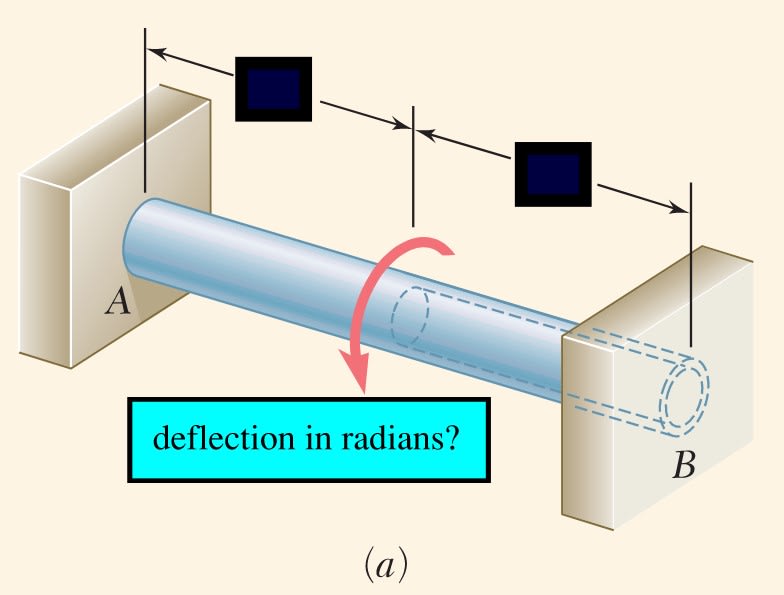
I have a column, fully fixed at both ends, very tall (~9metres)
It is subject to near nil compressive forces, or bending forces (no WL2/8 business). but it is very tall, ideally slender, and subject to a rotational load (from a big piece of signage which will me mounted off of the side, cantilevered out ~2 ft or so.)
the rotational force upon it will be quite large.
I am having trouble checking the column for rotational deflection. i have my old mechanics of materials textbooks out, but they are going deep into differential equations to solve, and don't have this particular case solved.
there must be some way to express/calculate the deflection in radians?
the idea is this sign shouldnt be flapping back and forth too much in the wind.

