Torsional stiffness of RC beam. 3

[Erickoso]

I've been trying to solve a moment distribution problem where I have a two span continuos beam framing into girders. I know for a fact that when I set up my distribution factors and carry overs I can't ignore the fact that those girders provide the supports of some torsional stiffness, so they can't be model as pinned supports but or fixed supports since the moment provided by those girder's contraints are not even near w*L^2/12. Then I've been trying to find a simple equation to determine those girders torsional stiffness to take into account for my distribution factors. However I can't find any simple eqn all I see are bunch of differential equations, I'm pretty sure engineers have come up with a much more simple and efficiente eqn for the torsional stiffness of a rectangural RC girder. Would you guys please help me find eqn?

 

[WARose]

The best resource (IMHO) is ACI SP-35. In particular, see the chapter on post-cracking stiffness, p.410 (for a example of it's calculation), and p.425 for a chart showing the ratio of cracked torsional stiffness to non-cracked (for various) parameters of reinforced concrete. (In general, the GKcracked/GKg ratio is equal to about 0.05 to 0.2 in my experience.)

 

[KootK]

I know for a fact that when I set up my distribution factors and carry overs I can't ignore the fact that those girders provide the supports of some torsional stiffness

I disagree. When beams crack torsionally, their torsional stiffness drops to something insanely low like 5% of the uncracked value. For the design of the girders themselves, I'd recommend looking into the concept of "compatibility torsion". Basically, you give your beam enough torsional reinforcing that it won't tear itself to pieces as it gives up it's torsional stiffness. And no more.

 

[Settingsun]

KootK, is there a structural problem with extra torsional reinf above minimum? Or just spending money needlessly?

 

[KootK]

No structural problem Steve. I can see how my choice of words may have lead to confusion though. Thanks for helping me to clarify.

 

[Erickoso]

I guess all I'm trying to find is reliable eqn to determine the torsional stiffnes of a RC girder to do my Moment distribution (look at the pictura I'm attaching) the only difference it's that the moments at both ends will not be zero anymore, there's some moment due to the girder torsional stiffness, typically people take it as wL^2/24 as partially fixed beam not 100% fixed but somehow fixed.I'm trying to be more precise and take into account the torsional stiffness of the girder, however I can't find a simple eqn it's not like flexural stiffness of a beam (4EI/L), McGregor in his book consider a beam as a hollow section, gives an eqn for the torsional stiffness would that work? the eqn is Kt=CG/L and C=4A0^2t/P0 Where A0 is the are enclosed by the shear flow taken as 2/3 of the concrete section perimeter, P0 is the perimeter of A0 and t is the thickness of the equivalent concrete tube. Any suggestion woulbe appreciated.

 

[hokie66]

Trying to be "precise" in this case is a fool's errand. Take KootK's advice, and just design the beam for pinned ends, nominal top reinforcement at the ends, then minimum torsional reinforcement for the girder.

 

[WARose]

SP-35 gives this expression (on p.398) for post-cracking stiffness in pure torsion:

GK[sub]cr[/sub]=(E[sub]s[/sub](b[sub]o[/sub]h[sub]o[/sub])[sup]2[/sup]A[sub]h[/sub]/u*s)*(1+m)

where:

E[sub]s[/sub]= Modulus of elasticity steel
b[sub]o[/sub]=Width between long. corner bars
h[sub]o[/sub]=Height between long. corner bars
u=2(b[sub]o[/sub]+h[sub]o[/sub])= perimeter
s=Hoop spacing
A[sub]h[/sub]=Area of one hoop leg

m=(A[sub]s[/sub]+A'[sub]s[/sub])s/(Ah*u)

A[sub]s[/sub]=Area of long. bottom steel
A'[sub]s[/sub]=Area of long. top steel

----------------------------------------------

You can always do the compatibility method discussed above......but be advised: you have to have a pretty good amount of torsional capacity in your beam to be able to accommodate it. ACI lays out the requirements.

 

[KootK]

@WARose: nice contribution. I was going to do the same so you've given me 20 minutes of my life back.

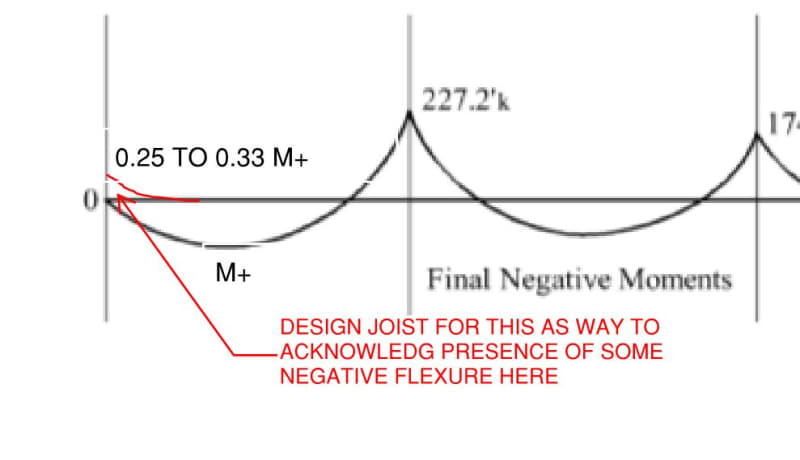
Trying to be "precise" in this case is a fool's errand.

@OP: that. Consider these sources of imprecision:

1) Per the graph below, response is related to reinforcement ratios and is all over the map.

2) Each joist will experience a different, torsion induced, end moment because:

2a) The girder will likely be torsionally uncracked in the middle where demand is low.

2b) The girder will likely be torsionally cracked but very torsionally stiff at the ends where direct struts into the supports will form.

Have fun trying to capture all of that and still capturing a shred of profit, right? For the design of the joist, see my sketch below for the "when in Rome" design procedure. Keep in mind that the combined experience of the folks advising your here is probably in the neighborhood of 75 yrs. Not. Our fist. Rodeo.

 

[Erickoso]

Thank you all for the help.