-
1
- #1
Hello All. Non-piping engineer here.
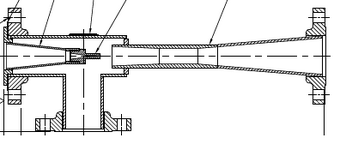
I am trying to determine what airflow I have through a section of pipe attached to what we call an exhauster. Searching for exhausters online doesn't come up with much, so I don't know how common they are or if they're known by some other term. Our exhauster is a T-shaped piping assembly with a venturi at the cross of the tee. An air line from a compressor is attached to one side of the tee and blows through the other side. A vacuum is created in the trunk of the tee, pulling air from below.
For an R&D project, we used this to pull hot air from the top of a furnace up through the tee, which had surface mount temperature sensors attached. For the analysis, I need to determine the flow rate through the trunk. I thought it would be a relatively simple calculation, and perhaps it is, but not being used to fluid calculations, I've not been able to get a clear idea what I need to do from all of the various resources I've looked at.
Air temperature is = ~1300F
Pipe = 1-1/2 Sch.40, 3' long, open at the bottom
Vacuum = 3 inHg (g)
I thought that it would be relatively trivial to convert vacuum to a pressure differential, but I'm not so confident that I've done it correctly.
Looking at this conversion table, I estimate that 3 inHg (g) may be around 10% vacuum, as well as around 13 psia.
Since I am exhausting to ambient, I can consider the pressure differential to be 14.7-13 psia = 1.7 psi
I'll assume no pressure gradient along the pipe for so short a length, and no friction factor for the same reason.
I've run across many different proposals on how to solve this, but using Bernoulli's Equation seems that it would be sufficient.
Let me know if you have a better way to determine the flow rate for these conditions.
I am trying to determine what airflow I have through a section of pipe attached to what we call an exhauster. Searching for exhausters online doesn't come up with much, so I don't know how common they are or if they're known by some other term. Our exhauster is a T-shaped piping assembly with a venturi at the cross of the tee. An air line from a compressor is attached to one side of the tee and blows through the other side. A vacuum is created in the trunk of the tee, pulling air from below.
For an R&D project, we used this to pull hot air from the top of a furnace up through the tee, which had surface mount temperature sensors attached. For the analysis, I need to determine the flow rate through the trunk. I thought it would be a relatively simple calculation, and perhaps it is, but not being used to fluid calculations, I've not been able to get a clear idea what I need to do from all of the various resources I've looked at.
Air temperature is = ~1300F
Pipe = 1-1/2 Sch.40, 3' long, open at the bottom
Vacuum = 3 inHg (g)
I thought that it would be relatively trivial to convert vacuum to a pressure differential, but I'm not so confident that I've done it correctly.
Looking at this conversion table, I estimate that 3 inHg (g) may be around 10% vacuum, as well as around 13 psia.
Since I am exhausting to ambient, I can consider the pressure differential to be 14.7-13 psia = 1.7 psi
I'll assume no pressure gradient along the pipe for so short a length, and no friction factor for the same reason.
I've run across many different proposals on how to solve this, but using Bernoulli's Equation seems that it would be sufficient.
Let me know if you have a better way to determine the flow rate for these conditions.