Tuned mass damper for mitigation of force vibration

[ceo_of_vibe_ration]

Hello everyone,

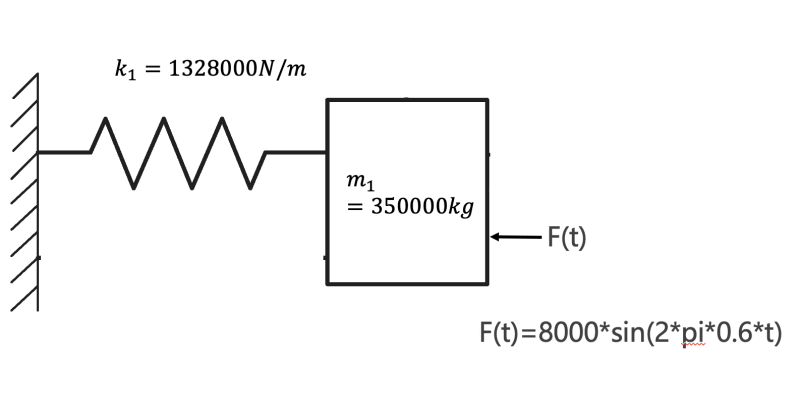
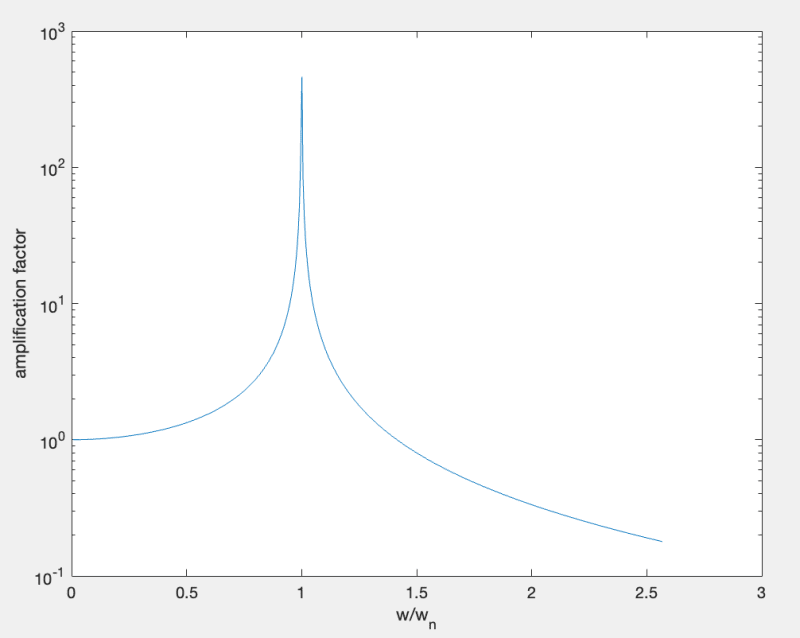
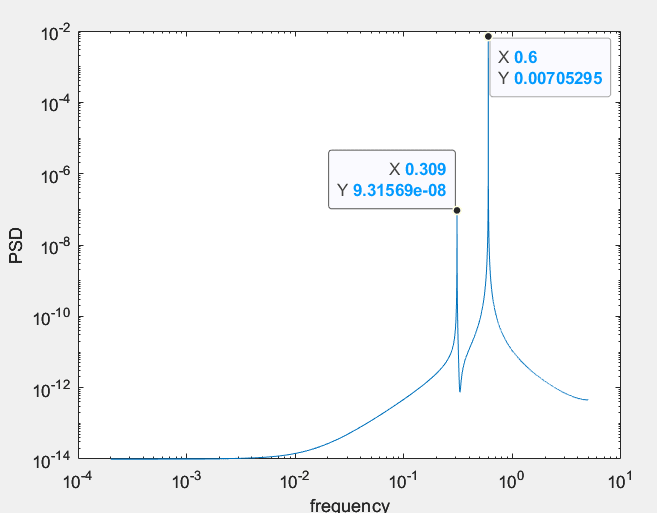
I have a simple question. Lets say a single degree of freedom system (SDOF) which consists of a spring and a mass is excited by an external force. The SDOF system has the eigenfrequency of 0.31 Hz and the external force is a periodic force with the frequency of 0.6 Hz. After decay of the transient effects, the frequency response function of the SDOF system should contain peaks at the system's eigenfrequency of 0.31 Hz and the 0.6 Hz excitation, right? Now I want to reduce the response at 0.6 Hz induced by the excitation with a tuned mass damper (TMD). The TMD also consists of a spring and a mass, and the eigenfrequency of the TMD is tuned to 0.6 Hz, as it should reduce this frequency. I built this configuration in ANSYS and calculated the SDOFs response under the influence of the TMD and the system's response at 0.6 Hz is even getting bigger. Am I understanding something wrong? Should a TMD with the tuned eigenfrequency not reduced the system's response at THAT frequency after the decay of the transient effects?
Another thought is the excitation induces resonance in the TMD and thus causing an amplification in the SDOF's system at the excitation frequency...

Best regards

 

[GregLocock]

"fter decay of the transient effects, the frequency response function of the SDOF system should contain peaks at the system's eigenfrequency of 0.31 Hz and the 0.6 Hz excitation, right?"
No
" I built this configuration in ANSYS and calculated the SDOFs response under the influence of the TMD and the system's response at 0.6 Hz is even getting bigger."
Then you have done something wrong
"Should a TMD with the tuned eigenfrequency not reduced the system's response at THAT frequency after the decay of the transient effects?"
Yes

You can calculate a 2dof steady state response by hand, to help you find the errors in your ANSYS

What are the details of the two systems?

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[ceo_of_vibe_ration]

Hey Greg,

the main system is a cantilevered beam with a lumped mass at the end. The beam itself does not have mass. The lumped mass experiences a periodic force excitation. The system can be expressed like follows:

For the SDOF system, the amplification function looks like this:

This is why you are disagreeing with me by saying the frequency response should contain two peaks, right?
But I modeled this system in ANSYS APDL, just like in the first picture. Within transient analysis, I applied the time variant load of F(t) and by PSD analysis of the SDOF displacement I get the following graph:

The only explanation for this I can think of is that the structure is excited with the 0.6 Hz excitation, but the response of the structure at 0.6 Hz is very small, even though it makes up a big part in the vibration overall. Thats why there is a peak at the 0.6 Hz frequency. And since the response of the system is small, by expanding the SDOF system with another spring-mass system with a natural frequency of 0.6 Hz, the main system is now getting excited, more by the second system than by the external excitation itself. Does this make sense?

Best regards

 

[GregLocock]

The SDOF linear system can only respond, in the steady state, at the frequency that it is being driven at. Hence there is something fundamentally wrong with your psd plot. How exactly are you calculating the PSD?

You also seem to be using some very undamped material, I wonder how your time based analysis gets to a steady state from that? real structures, even monolithic blocks of steel, have damping of the order of 0.1 %






Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[Denial]

I have a spreadsheet that models 2DOF systems.[ ] It might make your explorations a bit quicker and easier.[ ] You can download it from my website (

http://rmniall.com).

[sub][ ]—————————————————————————————————[/sub]
[sup]Engineering mathematician / analyst.[ ] See my profile for more details.[/sup]