dazz100
Industrial
- Oct 19, 2021
- 17
Hi
I am designing a TMD for a microscope application. The microscope is mounted on a standard computer monitor stand. In effect, this is a weight on the end of a cantilever. The lower arm acts as a torsion spring. Unsurprisingly, this has flex and undamped harmonic motion that makes the microscope difficult to use. Commercial stands from reputable manufacturers are no better.
In order to design a TMD, I need to characterize the motion. I have done this in 2 ways.
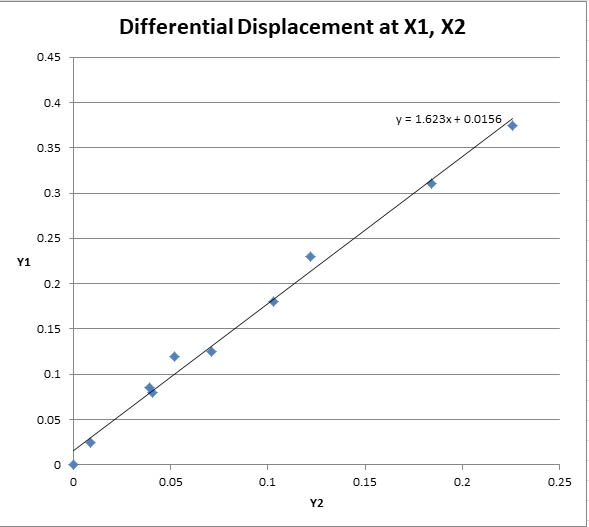
I have precisely measured the force and deflection to find the spring constant k. k is surprisingly linear and shows almost no hysteresis.
I measured the natural harmonic frequency of oscillation and weighed the mass of the scope. From this I have calculated k.
The problem is that the values of k measured by the two methods vary by a factor of about 7. Too much to be explained by measurement uncertainty. I think my simple cantilever spring model is the source of the gross error.
I am thinking the simplest way to adjust the model is to use an effective length of the cantilever. If I doubled the effective length, that would reduce the calculated harmonic frequency by 1/4x. It would increase the mass inertia by 4x.
Am I on the right track??
I am designing a TMD for a microscope application. The microscope is mounted on a standard computer monitor stand. In effect, this is a weight on the end of a cantilever. The lower arm acts as a torsion spring. Unsurprisingly, this has flex and undamped harmonic motion that makes the microscope difficult to use. Commercial stands from reputable manufacturers are no better.
In order to design a TMD, I need to characterize the motion. I have done this in 2 ways.
I have precisely measured the force and deflection to find the spring constant k. k is surprisingly linear and shows almost no hysteresis.
I measured the natural harmonic frequency of oscillation and weighed the mass of the scope. From this I have calculated k.
The problem is that the values of k measured by the two methods vary by a factor of about 7. Too much to be explained by measurement uncertainty. I think my simple cantilever spring model is the source of the gross error.
I am thinking the simplest way to adjust the model is to use an effective length of the cantilever. If I doubled the effective length, that would reduce the calculated harmonic frequency by 1/4x. It would increase the mass inertia by 4x.
Am I on the right track??