SouthSide08
Electrical
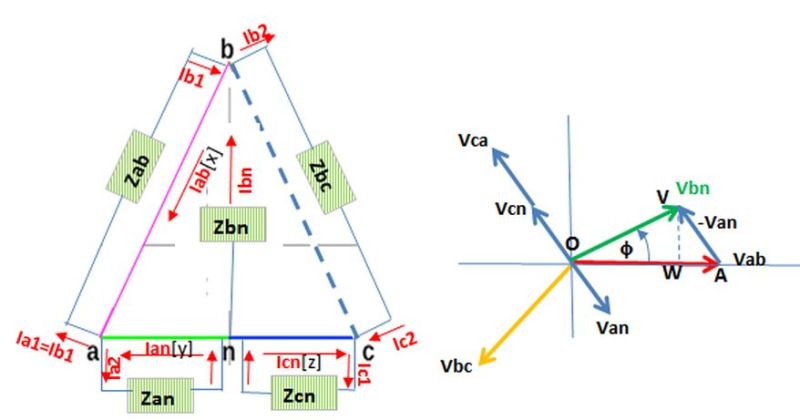
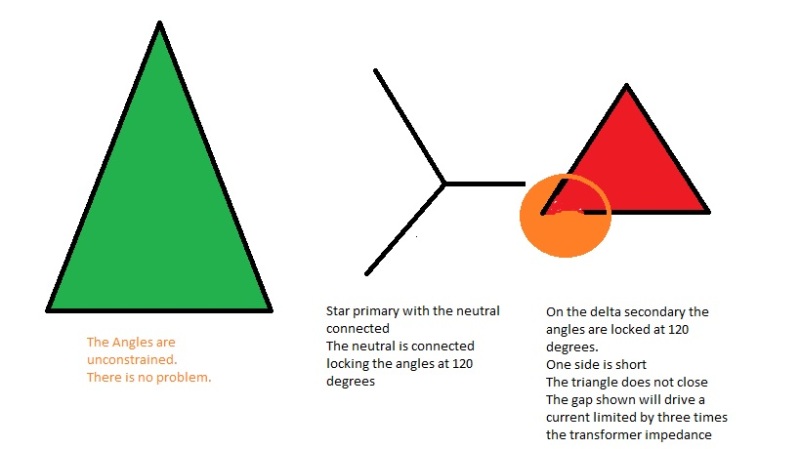
I am trying to solve line currents for a delta delta transformer using nodal analysis but couldn't arrive with the correct answer. The simple way I have done this before is to distribute kVA loads to individual phases then divide by the Voltage / Sqrt 3. Say we 3kVA load on phase AB, 4kVA on BC and 5kVA on AC. The system is Delta-Delta 2400 - 240Vac. What I would do is do a schedule and get the total kVA per phase. Phase A = 4kVA; Phase B = 3.5kVA; Phase C = 4.5kVA. I would then divide each phase by 240/sqrt3 to get the individual line currents which result to IA = 28.87A IB=25.26A IC=32.48A
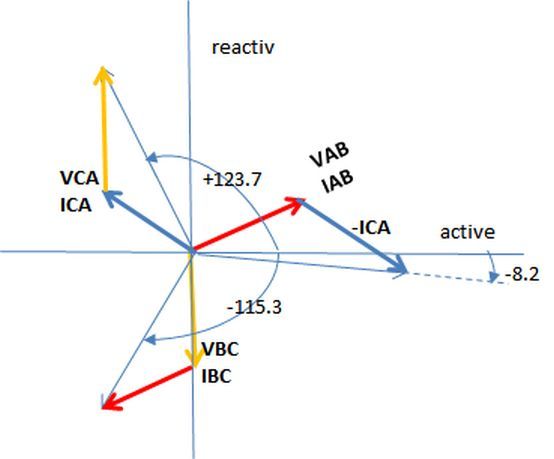
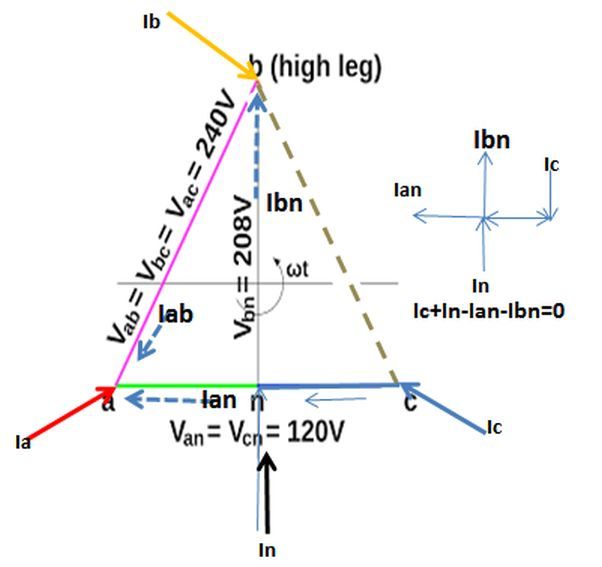
I believe this is a correct and simple method but I would like to solve this using nodal analysis to get the phase angles on the individual currents as well. A spreadsheet mentioned on thread238-156846 has an answer for this type of loading but the link mentioned on the thread does not work anymore. I was hoping somebody can give me the spreadsheet or if not help me on how to solve this using nodal analysis. Also interested on how to do the calculations when dealing with mid-tap single phase transformers. Appreciate any comments and advice on this matter.
Respectfully.
I believe this is a correct and simple method but I would like to solve this using nodal analysis to get the phase angles on the individual currents as well. A spreadsheet mentioned on thread238-156846 has an answer for this type of loading but the link mentioned on the thread does not work anymore. I was hoping somebody can give me the spreadsheet or if not help me on how to solve this using nodal analysis. Also interested on how to do the calculations when dealing with mid-tap single phase transformers. Appreciate any comments and advice on this matter.
Respectfully.

![[blush] [blush] [blush]](/data/assets/smilies/blush.gif)