Unbraced Length of Compression Chords in 3D truss 1

[Stickengnerd]

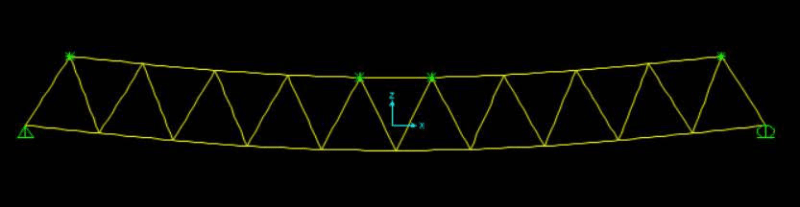
In working through the design of a (3) dimensional truss with an inverted triangular cross section and a span of nearly 100ft, what would the unbraced length of the (2) top chord compression members be? Is it accurate to consider the unbraced member length the distance between the diagonals, in both the Lz and Ly directions? Or do you have to consider the unbraced member length the entire length of the truss? Or perhaps the answer is somewhere in between, using the distance between the diagonals with a multiplication factor? Note: The roof deck will not help in this situation, as it is a remodel intended to remove columns below, and the roof deck is to be suspended below the truss.

Does anyone have any recommendations of good texts or papers to read on (3) dimensional truss design / box truss design that might address this, or anything else I'm not thinking of?

https://res.cloudinary.com/engineering-com/image/upload/v1581537489/tips/Truss_apujbm.jpg

 

[KootK]

Some more thoughts on my last post...

1) For a 2D truss, and for the vertical-ish sides of a 3D truss, I stand by my previous post.

2) For the horizontal top of a 3D detlta truss, it gets a bit murkier I think. There is still no net-compression on the cross section (bottom chord rides along laterally) so that part of the logic stands. However, the degree to which the bottom, tension chord rides along with the top, compression chords is imperfect. I've come to view this as another perspective on lateral torsional buckling (LTB), both as it pertains to trusses and to beams. In a way, I think that LTB can be thought of as the tension chord/flange failing to perfectly ride along laterally with the compression flange and, therefore, failing impose cross sectional balance to the P-Big Delta demands on the individual chords that arise from internal actions. Kind of another telling of the story shown below.

 

[JoshPlumSE]

KootK -

Let's start off thinking about a portal frame, the simplest form of P-Delta. Right?
If you have no vertical load, put only lateral load, then one column in compression and one is in tension. Therefore, T*Delta = C*Delta and the stiffening effect of the tension T, negates the amplification effect of the compression C. It's only when there is a significant vertical load where both columns are in compression (or the tension column force has a much lower magnitude than the compression column) that the P-Big Delta amplification can become significant.

This is sort of what you're saying, right? That a 2D truss loaded purely in plane with no ability to deflect out of plane imparts compression in the top chord that is essentially equal to the tension in the bottom chord. Therefore, P-Big Delta effects don't occur. Any 2nd order amplification of the top chord deflection is negated by stiffening caused by the 2nd order deflections on the tension chord. Is that correct?

Your assertion might be a slight over simplification, but I would agree in principal. I think you can still get some differences between a linear and P-Delta analysis. But, it's probably small and due to some geometric differences between the top and bottom chord. The top chord can obviously still buckle in plane, but it will due be more to a P-little delta effect between the brace points.

I built the model shown below in SAP2000 and ran a Linear and Non-Linear analysis.

The P-Big Delta amplification existing, but it was very low.... on the order of 0.05%. Then it increased to .13% when I increased the load by a factor of 5.

Later this afternoon (or tonight) I'll respond to the portion of the question that relates to a 3D truss with a lateral load applied to the top chord.

 

[KootK]

Let's start off thinking about a portal frame, the simplest form of P-Delta. Right?

Right, and that is a very instructive example.

This is sort of what you're saying, right?

Therefore, P-Big Delta effects don't occur. Any 2nd order amplification of the top chord deflection is negated by stiffening caused by the 2nd order deflections on the tension chord. Is that correct?

Precisely; so far, so good. And thanks for the FEM verification. Love that. No rush at all but I very much look forward to your thoughts on the rest. I'll be out of town until Sunday working a V-day plan.

 

[JoshPlumSE]

KootK -

Before I finish the 3D truss example, I went through and re-read that old thread and some extra thoughts came to mind related to the 2D truss example.

I already mentioned this, but thought I should elaborate about geometric differences between top and bottom chord. This could be:
a) Different member sizes or lengths.
b) Even with the same member size, the TauB could be different due to tension vs compression.
c) In my 2D truss above, the nodes are offset. Meaning the axial forces won't quite match. If the chords were totally symmetric, with the same lengths and X bracing between them, I don't think the P-Big Delta effect would occur.
d) My model isn't the best example since I applied a distributed load to the top chord. That alone causes a geometric difference in the top and bottom chords. In order to perfectly test what KootK's talking about, I would have had to apply the loads at the panel joints of the truss.

So, even though the P-Big Delta effects are small, I believe I could get them to go down further if I was really, really careful with the geometric differences and the loading.

 

[JoshPlumSE]

KootK -

Okay, now the 3D truss similar to the 2D truss, but with 2 top chords and a single bottom chord. Gravity load puts BOTH top chords in compression. So, if I apply a lateral notional load to the top chords. They're still both in compression (because gravity force is dominant), but one has a little more and one has a little less. This is akin to the portal frame where both columns are in compression due to gravity load, but the amount of compression is unequal due to the lateral load. Maybe a braced frame would be a more accurate example since we have the top chords trussed together with diagonals.

Now, P-Big Delta effects on these top chords tend to amplify any sideways deflection due to the notional load. And, the bottom / tension chord doesn't really come into play since it's not really deflecting in the lateral direction. So, it's not really providing much stiffening.

This bears out in the FEM model as well where I was seeing something like a 0.7% amplification due to P-Big Delta. Now, in both cases (2D and 3D), I was using what I thought was a reasonably flimsy chord. So, your intuition is pretty good..... P-Big Delta effect is not very significant at reasonable force levels. It exists, like it would exist in braced frame structures, but it is reasonably low.

Now, my chords were pretty flimsy. So, I imagine they would fail a code check based on using an unbraced length between panel points. And, would get killed by a P-little delta analysis.

 

[Settingsun]

Josh, what are the details of the 3d truss? Is it bending about its major axis (ie deep, narrow cross section) or minor axis (shallow, wide)? If major axis, what is the L/r_y value?

To help explain, is it susceptible to lateral torsional buckling if considered as a hollow-section beam?

 

[Stickengnerd]

Thanks for the analysis JoshPlumSE. That was very helpful.

Out of curiosity, is there a balance point where the width between the top chords in compression is optimized compared to the trusses height? I've designed the truss at almost a 1:1 ratio. It's nearly as wide as it is tall (This was done simply because most of the ones I see have this geometry), and in this case, I don't see big P-delta coming anywhere close to controlling. But now I'm curious if there is a height to width ratio, say 2:1, that is more efficient. Seems that since the global buckling has such a tiny effect on the design that the overall width could be reduced, thereby reducing the amount of material. I haven't had the chance to give it a shot yet.

Thanks for your input.

 

[KootK]

Architecturally, I've seen a lot of these with what look to be 30 angles inside the vee. If cost is the main driver, I'd consider equilateral. A bit more tonnage on the webbing but, then, every web can be the same.