Hello everyone!
I'd like to understand the meaning and practical interpration of complex input and output in harmonic/frequency response FEA.
Let's start with input - each load in this type of analyses can be defined with an imaginary component (F=F_Re+iF_Im). From what I've read, it's out-of-phase load. But what does it mean in practice? Does it always correspond to phase angle of 90 degrees so when one sine wave is at zero, the other one is at its peak as shown here?
It makes sense when there are two loads (like Fx with real component and Fy with imaginary component) - then the aforementioned two sine waves are time variations of both loads. But what when there's only Fx with real (in-phase) and imaginary (out-of-phase) component?
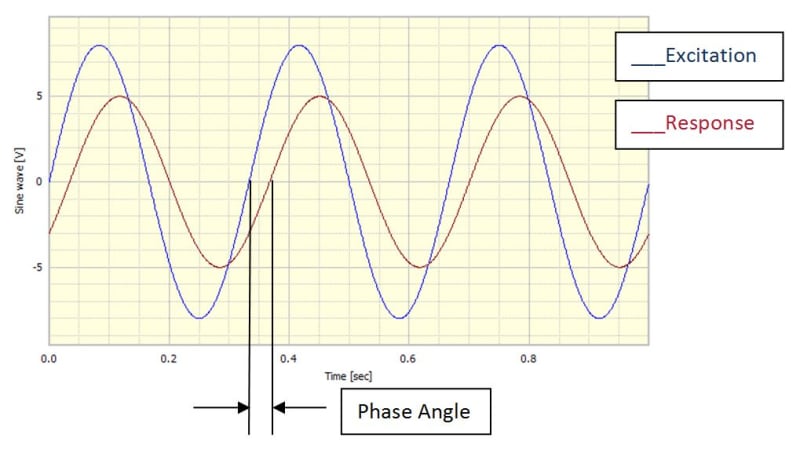
Now when it comes to output, which is much more complicated - it can be expressed in two different forms - magnitude and phase angle or real and imaginary. As I understand, magnitude simply means amplitude of the sine wave of the response. Phase angle is more tricky. Is it just the offset between the two sine waves (load and response) like in the picture below?
Source:
And is it true that a phase angle of 180 degrees corresponds to the case when sine waves are opposite (when one is at its peak, the other one is at its trough as shown on the first referenced website)?
Real and imaginary representation of the results is the most difficult to understand for me and the referenced blog post doesn't really help. I would assume that real is the same as mangitude in the first representation but I can be wrong. What about the imaginary part? Could you explain its practical/physical meaning in simple words?
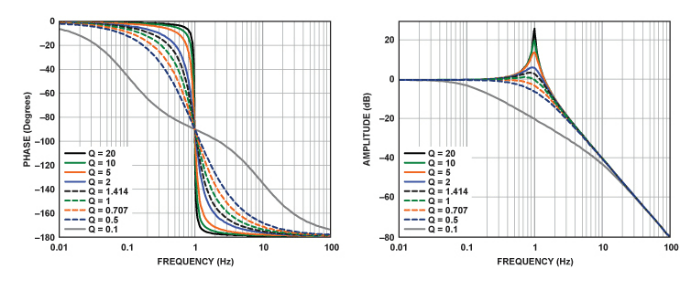
I've also heard that a phase angle of 90 degrees corresponds to natural frequency. Is it really the case? Why?
I'd like to understand the meaning and practical interpration of complex input and output in harmonic/frequency response FEA.
Let's start with input - each load in this type of analyses can be defined with an imaginary component (F=F_Re+iF_Im). From what I've read, it's out-of-phase load. But what does it mean in practice? Does it always correspond to phase angle of 90 degrees so when one sine wave is at zero, the other one is at its peak as shown here?
It makes sense when there are two loads (like Fx with real component and Fy with imaginary component) - then the aforementioned two sine waves are time variations of both loads. But what when there's only Fx with real (in-phase) and imaginary (out-of-phase) component?
Now when it comes to output, which is much more complicated - it can be expressed in two different forms - magnitude and phase angle or real and imaginary. As I understand, magnitude simply means amplitude of the sine wave of the response. Phase angle is more tricky. Is it just the offset between the two sine waves (load and response) like in the picture below?

Source:
And is it true that a phase angle of 180 degrees corresponds to the case when sine waves are opposite (when one is at its peak, the other one is at its trough as shown on the first referenced website)?
Real and imaginary representation of the results is the most difficult to understand for me and the referenced blog post doesn't really help. I would assume that real is the same as mangitude in the first representation but I can be wrong. What about the imaginary part? Could you explain its practical/physical meaning in simple words?
I've also heard that a phase angle of 90 degrees corresponds to natural frequency. Is it really the case? Why?