-
1
- #1
ChickenBake
Structural
- Jun 26, 2024
- 6
I'm stuck on a thought experiment regarding development length and I'm wondering if I can get some guidance.
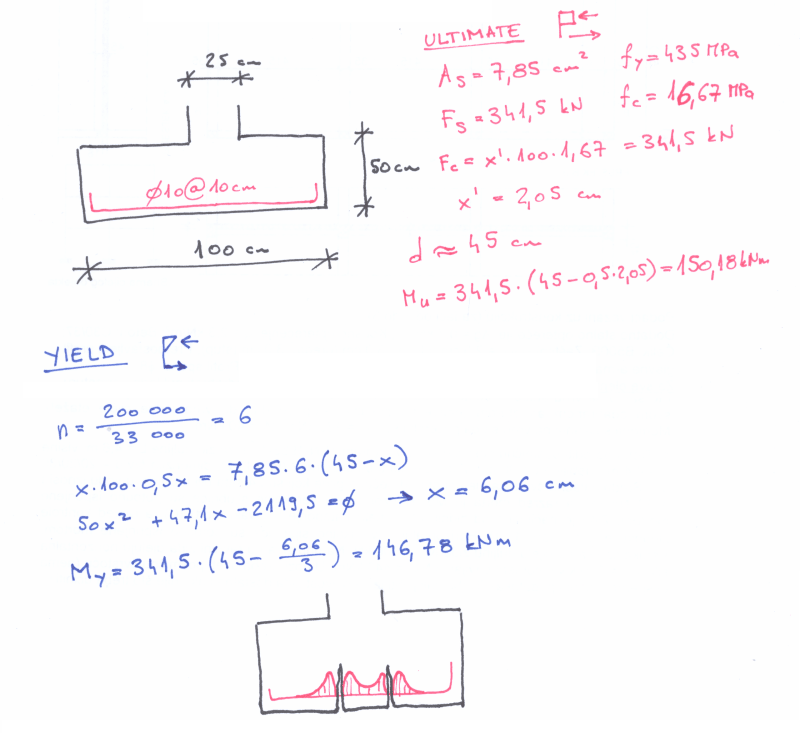
Consider a simple column footing. Assume that the moment at the critical section, Mu, is exactly equal to φMn. Also, assume that the footing section is tension-controlled.
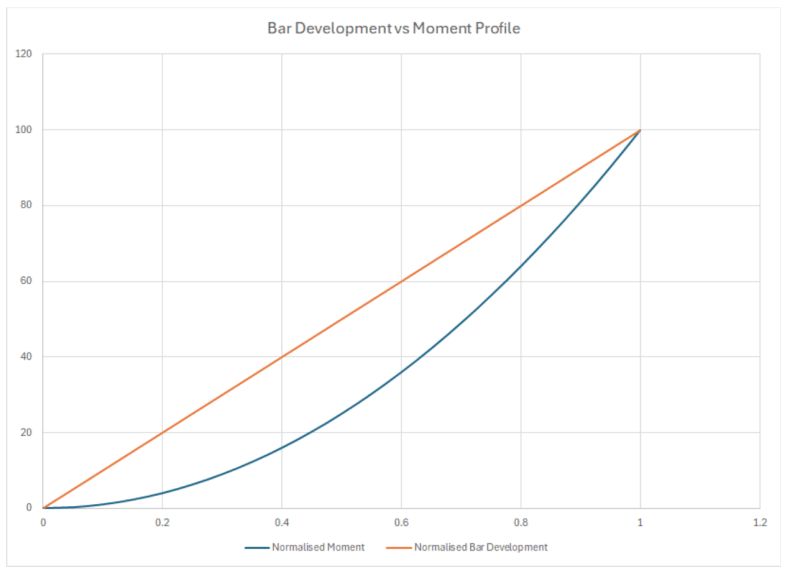
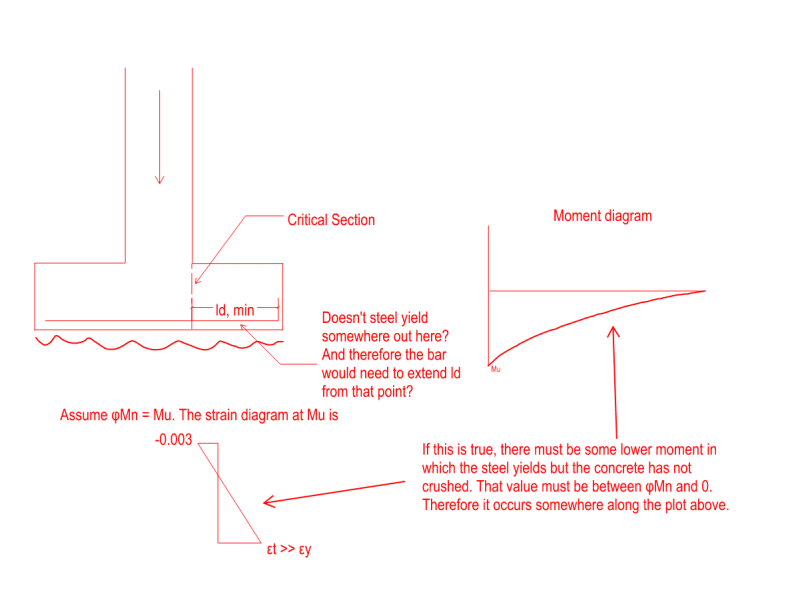
It follows from the assumptions that the strain at the critical section is far beyond the yield strain. Because the moment tapers down to 0 at the tip of the footing, and the yield moment must be some value between Mu and 0, there is some section, between the tip and the critical section, where the steel has yielded.
ACI requires the force in steel reinforcing to be developed on both sides of the plane in all cases. Yet anytime I see calcs for a footing, development is only checked at the critical section. Shouldn't it actually be checked at the point the bar yields? Am I wrong in my assumptions somewhere?
I have attached brief sketch of this below.
Consider a simple column footing. Assume that the moment at the critical section, Mu, is exactly equal to φMn. Also, assume that the footing section is tension-controlled.
It follows from the assumptions that the strain at the critical section is far beyond the yield strain. Because the moment tapers down to 0 at the tip of the footing, and the yield moment must be some value between Mu and 0, there is some section, between the tip and the critical section, where the steel has yielded.
ACI requires the force in steel reinforcing to be developed on both sides of the plane in all cases. Yet anytime I see calcs for a footing, development is only checked at the critical section. Shouldn't it actually be checked at the point the bar yields? Am I wrong in my assumptions somewhere?
I have attached brief sketch of this below.