Unload- reload, get Young's modulus and poisson's ratio.

[vektorrum]

Hello!

I'm a student and need help getting effective Young's modulus (E´50) and poisson's ratio (v´) from a unload reload drained test of clay material. See the figure below.

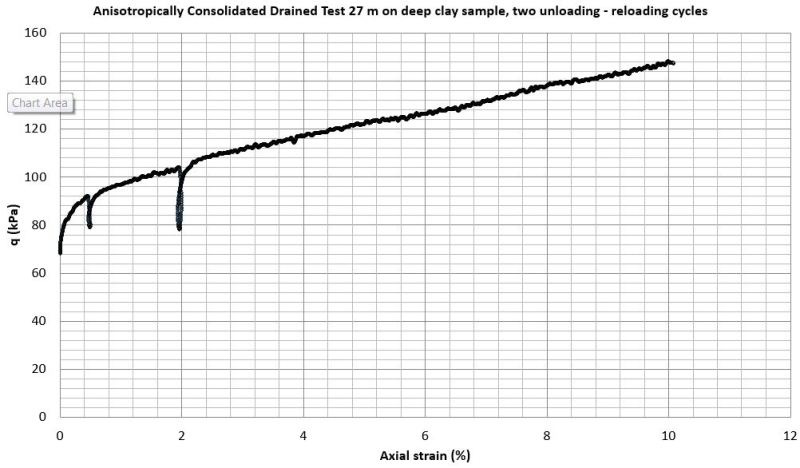
Would be really grateful if someone can helo me with this, been sitting whole day trying to figure out this.

Best regards,
Viktor

 

[LRJ]

E50 is a secant modulus (the secant stiffness at 50% of the stress difference). To get this for an anisotropic test (such as your example above) you need to determine the change in stress and change in strain at the point corresponding to 50 % of the stress difference (which looks to be at approximately: q = (150 - 70)/2 + 70 = 110 kPa). The strain at q = 110 kPa is approximately 2.5%, so E50 therefore looks like it will be something like 110 kPa / 0.025 = 4400 kPa.

Nonetheless, the emphasis on the unload-reload loops makes me think they are not actually looking for E50, or they have their terminology mistaken. Stiffness is simply the change in stress over the change in strain (i.e. the gradient of the stress-strain curve). From this definition, determining any stiffness should be straightforward.

You can't get Poisson's ratio from the graph you have shown us. You need radial strain which you would typically get from volumetric strain in a drained triaxial test.

 

[vektorrum]

Thank you for a great answer!

Another quick question, can we determine E' from the graph as well?
Or should E' be equal to E'50 which I have been read is common to assume?

Bests regards,
Viktor

 

[LRJ]

E' is the 'drained' Young's modulus (also noted as E_d), which is just the stiffness in the graph above because it is a drained test. Moreover, you wouldn't be able to get E_u (the 'undrained' Young's modulus) from the above test because it is not an undrained test.

E'50 is the E50 I referred to in my previous post. In the context discussed (i.e. with emphasis on the unload-reload loops) I would expect they are asking you what the stiffness of those loops is. That stiffness is E'.

Do you have volumetric strain data with this test? If so, you can get the radial strain from axial and volumetric strain, then derive Poisson's ratio.

 

[Okiryu]

I do not have experience with anisotropic tests, but assuming that "q" is applied in the axial direction, it surprises me that the stress-strain curve is not passing thru the origin. Is this real data?

 

[LRJ]

Anisotropically consolidated tests, by definition, have a difference between sigma1 and sigma3 at the end of consolidation/start of shearing. Moreover, if sigma1 equalled sigma3 it would be an isotropically consolidated test. As sigma1 and sigma3 are not equal, q is not equal to zero.

 

[Okiryu]

Thanks LRJ. Theoretically it sounds right. I was just surprise that with a deviator stress of about 70 kPa, you can get 0% strains.