vektorrum
Civil/Environmental
- Jan 27, 2016
- 3
Hello!
I'm a student and need help getting effective Young's modulus (E´50) and poisson's ratio (v´) from a unload reload drained test of clay material. See the figure below.
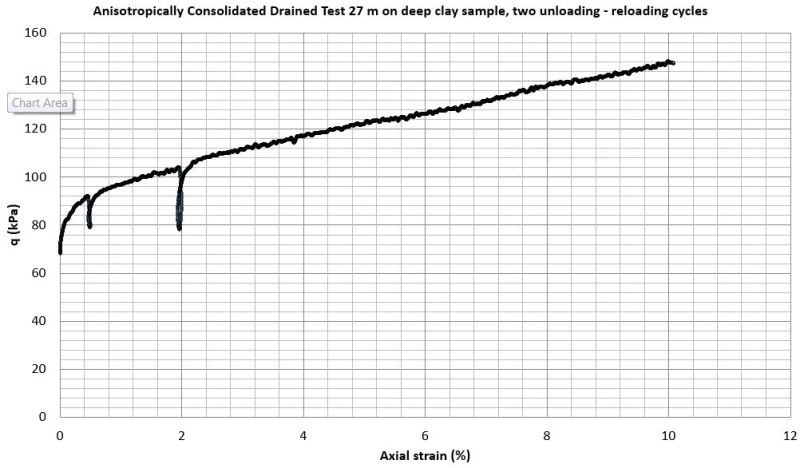
Would be really grateful if someone can helo me with this, been sitting whole day trying to figure out this.
Best regards,
Viktor
I'm a student and need help getting effective Young's modulus (E´50) and poisson's ratio (v´) from a unload reload drained test of clay material. See the figure below.

Would be really grateful if someone can helo me with this, been sitting whole day trying to figure out this.
Best regards,
Viktor
