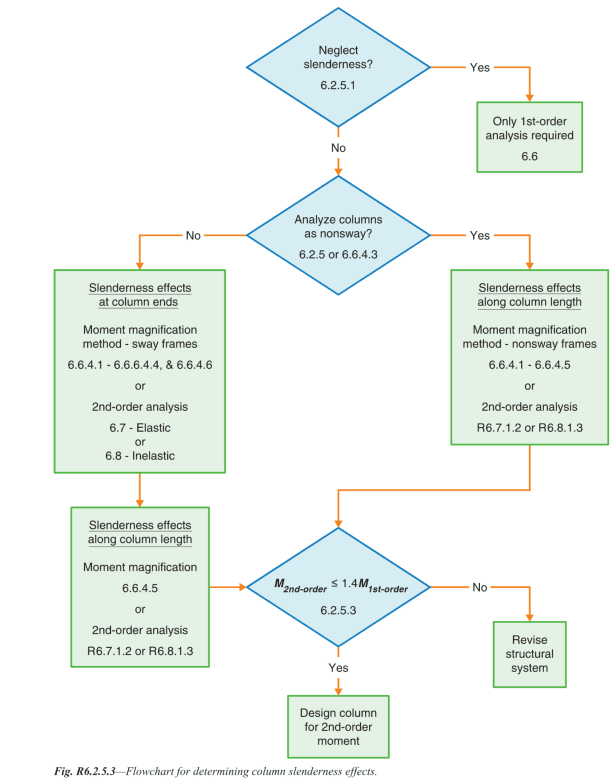
Hi all,
I'm trying to understand the difference between steel and concrete design for buckling, specifically the 'column curve' for steel when applied to unbraced frames. Here's how I understand the two design processes:
1) Both steel and concrete design use lateral loads to simulate the construction tolerances - the frames aren't perfectly vertical.
2) Both steel and concrete use reduced stiffnesses in the analysis to account for the respective departures from perfect elasticity of nominal cross-sections. For steel, the reduction accounts for premature yielding due to residual stressed. In concrete, the reduction accounts for cracking and creep.
3) Both steel and concrete use second-order analysis to account for P-Delta effects (capital Delta).
4) Both steel and concrete use second-order analysis (subdivided analysis members) or moment magnification to account for P-delta (lower-case delta).
5a) For concrete, the columns not being perfectly straight between levels is accounted for by using a minimum (first order) bending moment that has to have moment magnification applied. For an unbraced frame subject to lateral loads, this usually doesn't govern so the axial force (P_ULS) and bending moment (M_ULS)from Steps (3) and (4) are checked against the cross-section interaction diagram. For the case of an unbraced frame under lateral loading, Step (3) usually governs (i.e. the end moments rather than the mid-height moment).
5b) For steel, the columns not being perfectly straight between levels is accounted for by the column curve which reduces the axial capacity compared to the pure cross-section capacity.
So, in effect, there's an extra step in steel design for the lateral load case(s) in unbraced frames. What's not clear to me is whether that's just extra conservatism or whether concrete design misses something.
I understand how the column curve comes into the design of columns in braced frames because they have small bending moments so the P-delta (lower case) effect at the column mid-height due to the column not being straight is significant, but the concrete method makes more sense to me for unbraced frames where the mid-height moment is small and the additional moment due to non-straight initial shape will not make mid-height moment larger than at the ends.
I'm thinking that the column curve applied to unbraced frames is a hangover from the days when the effective length was used instead of lateral loads in Step (1) because the end moments were underestimated by the analysis due to no allowance for the frame to be non-vertical as opposed to the current use for non-straight.
Agree/disagree?
I'm trying to understand the difference between steel and concrete design for buckling, specifically the 'column curve' for steel when applied to unbraced frames. Here's how I understand the two design processes:
1) Both steel and concrete design use lateral loads to simulate the construction tolerances - the frames aren't perfectly vertical.
2) Both steel and concrete use reduced stiffnesses in the analysis to account for the respective departures from perfect elasticity of nominal cross-sections. For steel, the reduction accounts for premature yielding due to residual stressed. In concrete, the reduction accounts for cracking and creep.
3) Both steel and concrete use second-order analysis to account for P-Delta effects (capital Delta).
4) Both steel and concrete use second-order analysis (subdivided analysis members) or moment magnification to account for P-delta (lower-case delta).
5a) For concrete, the columns not being perfectly straight between levels is accounted for by using a minimum (first order) bending moment that has to have moment magnification applied. For an unbraced frame subject to lateral loads, this usually doesn't govern so the axial force (P_ULS) and bending moment (M_ULS)from Steps (3) and (4) are checked against the cross-section interaction diagram. For the case of an unbraced frame under lateral loading, Step (3) usually governs (i.e. the end moments rather than the mid-height moment).
5b) For steel, the columns not being perfectly straight between levels is accounted for by the column curve which reduces the axial capacity compared to the pure cross-section capacity.
So, in effect, there's an extra step in steel design for the lateral load case(s) in unbraced frames. What's not clear to me is whether that's just extra conservatism or whether concrete design misses something.
I understand how the column curve comes into the design of columns in braced frames because they have small bending moments so the P-delta (lower case) effect at the column mid-height due to the column not being straight is significant, but the concrete method makes more sense to me for unbraced frames where the mid-height moment is small and the additional moment due to non-straight initial shape will not make mid-height moment larger than at the ends.
I'm thinking that the column curve applied to unbraced frames is a hangover from the days when the effective length was used instead of lateral loads in Step (1) because the end moments were underestimated by the analysis due to no allowance for the frame to be non-vertical as opposed to the current use for non-straight.
Agree/disagree?