Matte StrEng
Civil/Environmental
Hi! I perform moving load analysis using Sprung mass (SDOF system) for bridge modal identification (called drive-by monitoring) from the vehicle responses. I face a problem when using more than one contact point (like two quarter cars).
The bridge (25m) and the approach slab (2m) are modelled with a 2D Bernoulli beam element. When one Contact Point representing a sprung mass system at 5m/s is used in Model 2 and Model 3 (see Picture 2), regardless of whether the sprung mass enters the bridge coming from the approach slab or starts moving at the bridge support, both results are very coherent. It is only observed that there is a slight difference between the acceleration responses. The higher acceleration of the sprung mass in Model 2 can be due to the impact of the Contact point that comes from the rigid platform to the bridge. The jump in the acceleration when entering the bridge is reasonable and does not affect the accuracy of the results. However, when two sprung mass systems are used in Model 1 (see Picture1) (despite having the same properties as models 2 and 3), an acceleration peak (60 m/s2) occurs when the back contact point is about to enter the bridge. This occasion twists all the results. Moreover, in Model 1, I also tried to use the back sprung system (in the approach slab) without mass and force, then the same acceleration peak occurred. Using finer mesh does not solve the issue as well.
What can be the solution to this problem?
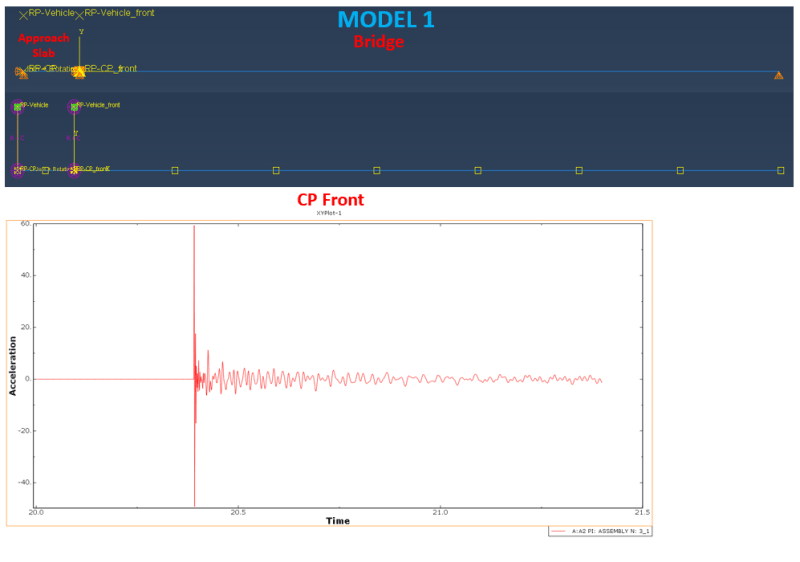
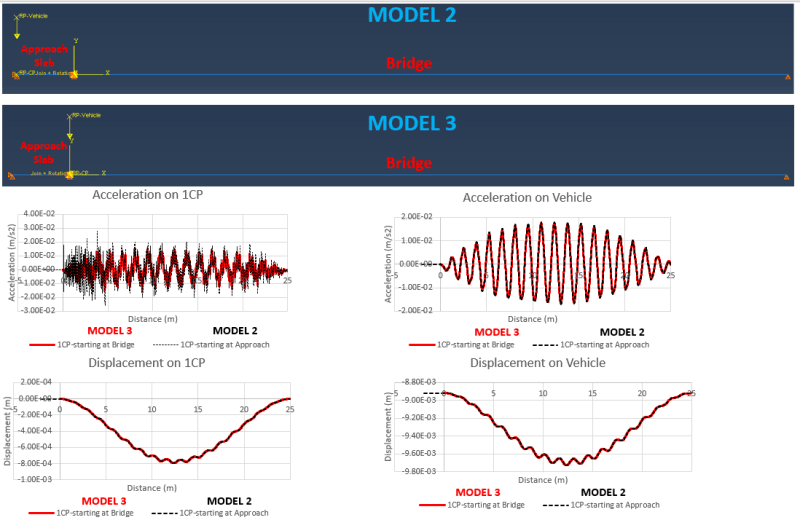
The bridge (25m) and the approach slab (2m) are modelled with a 2D Bernoulli beam element. When one Contact Point representing a sprung mass system at 5m/s is used in Model 2 and Model 3 (see Picture 2), regardless of whether the sprung mass enters the bridge coming from the approach slab or starts moving at the bridge support, both results are very coherent. It is only observed that there is a slight difference between the acceleration responses. The higher acceleration of the sprung mass in Model 2 can be due to the impact of the Contact point that comes from the rigid platform to the bridge. The jump in the acceleration when entering the bridge is reasonable and does not affect the accuracy of the results. However, when two sprung mass systems are used in Model 1 (see Picture1) (despite having the same properties as models 2 and 3), an acceleration peak (60 m/s2) occurs when the back contact point is about to enter the bridge. This occasion twists all the results. Moreover, in Model 1, I also tried to use the back sprung system (in the approach slab) without mass and force, then the same acceleration peak occurred. Using finer mesh does not solve the issue as well.
What can be the solution to this problem?


