Hello everyone!
I'm working on a simple benchmark problem for FEA software. It involves the following simplified model of a bolted joint:
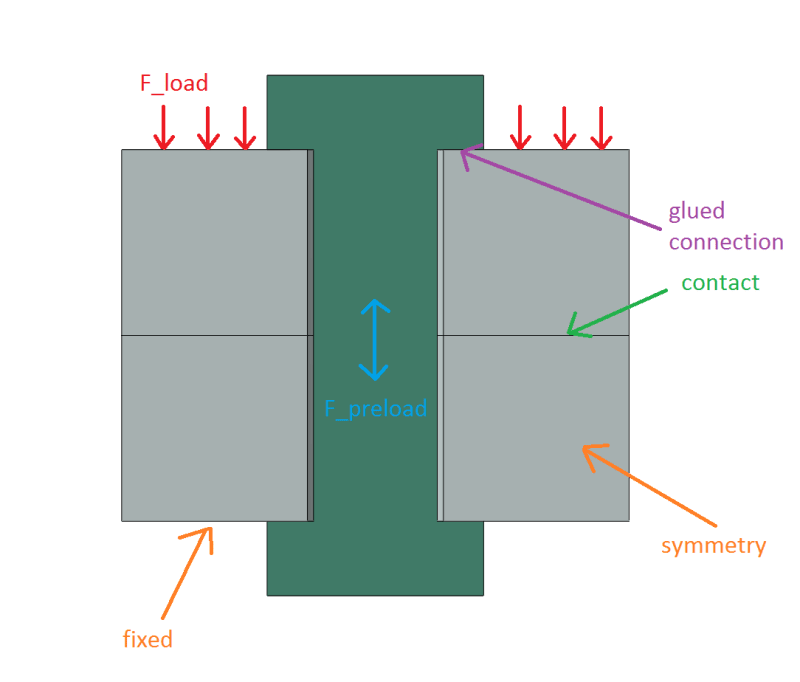
It's not a real bolt, the geometry was made up by me. For now, I only want to test the general procedure.
This FEA model represents half of the whole joint. The bolt is a single part (shank + head + nut), perfectly bonded (glued/tied) to both rings forming the joint. Pretension force F_preload = 200 N is applied to the bolt in the first step of the analysis while in the second step, pretension force is disabled and actual compressive load F_load = 400 N is applied to the top surface of the upper ring. Of course the values above are half of the load applied to the full joint. The bottom surface of the lower ring is fixed. Frictionless contact is defined between the rings. My goal for now is to obtain the force in the bolt at the end of the analysis (after preload stops working and actual compressive load is applied). From the analysis I get around 188 N (I confirmed that by running an analysis without symmetry). But the problem is that I can't get good agreement with analytical calculations. My first approach was simply superposition of the stresses (F_preload/A_bolt - F_load/A_ring) but it gave me around 171 N so I started searching for more accurate approach. I've found a nice article describing the use of a standard method known from literature (accounting for bolt and joint stiffnesses and involving equivalent cylinder to calculate the stiffness of the joint) and comparing it with FEA:
This article uses formulas from "Introduction to the Design and Behavior of Bolted Joints" by J.H. Bickford. Here are my calculations based on that (for the full model):
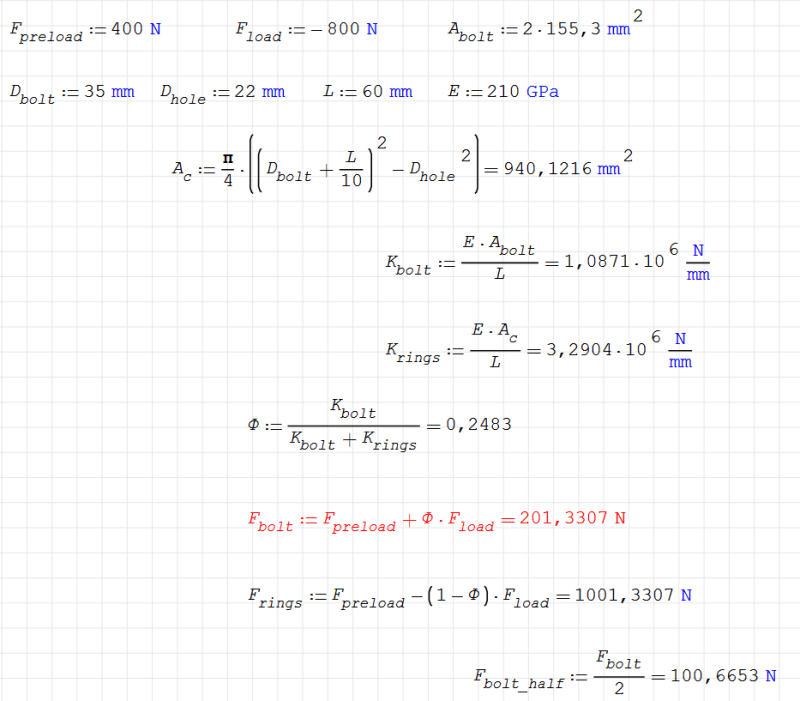
where: D_bolt - diameter of contact between bolt head and joint (it's a ring so a bit confusing to me), L - height of bolt shank/joint, D_hole - diameter of the hole in the joint, A_bolt - cross-sectional area of the bolt.
As you can see, bolt force according to this is around 201 N (100 N for model utilizing symmetry) so way too low. I thought that the problem might be caused by the fact that those equations are meant for tension, not compression but I can't get agreement for tension either. I've also tried applying F_load to the top surface of the bolt head like in the article but it didn't help. There's always such a large difference. I feel that I'm making some silly mistake somewhere here. Do you know what can be the cause of the problem? I will be really grateful for any help.
I'm working on a simple benchmark problem for FEA software. It involves the following simplified model of a bolted joint:

It's not a real bolt, the geometry was made up by me. For now, I only want to test the general procedure.
This FEA model represents half of the whole joint. The bolt is a single part (shank + head + nut), perfectly bonded (glued/tied) to both rings forming the joint. Pretension force F_preload = 200 N is applied to the bolt in the first step of the analysis while in the second step, pretension force is disabled and actual compressive load F_load = 400 N is applied to the top surface of the upper ring. Of course the values above are half of the load applied to the full joint. The bottom surface of the lower ring is fixed. Frictionless contact is defined between the rings. My goal for now is to obtain the force in the bolt at the end of the analysis (after preload stops working and actual compressive load is applied). From the analysis I get around 188 N (I confirmed that by running an analysis without symmetry). But the problem is that I can't get good agreement with analytical calculations. My first approach was simply superposition of the stresses (F_preload/A_bolt - F_load/A_ring) but it gave me around 171 N so I started searching for more accurate approach. I've found a nice article describing the use of a standard method known from literature (accounting for bolt and joint stiffnesses and involving equivalent cylinder to calculate the stiffness of the joint) and comparing it with FEA:
This article uses formulas from "Introduction to the Design and Behavior of Bolted Joints" by J.H. Bickford. Here are my calculations based on that (for the full model):
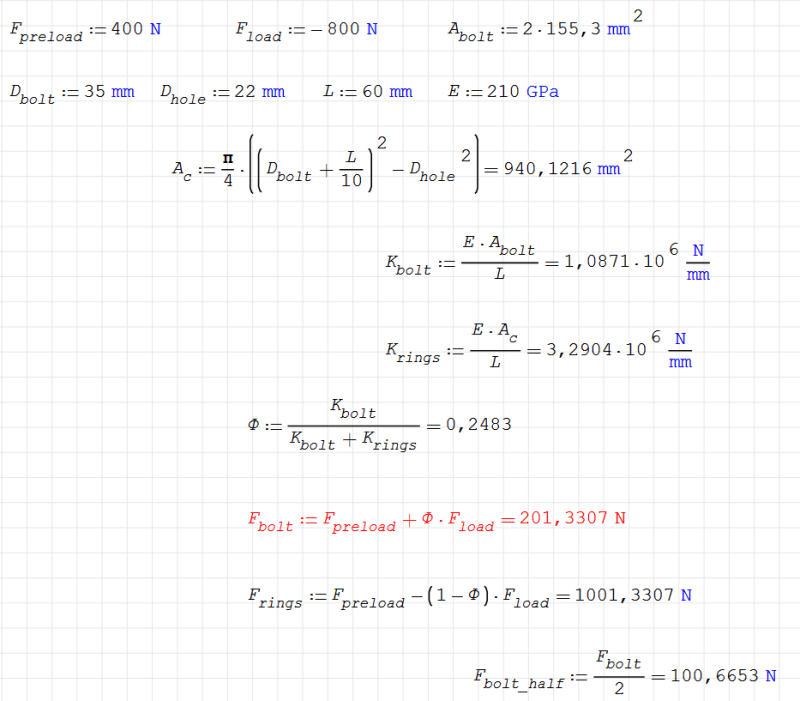
where: D_bolt - diameter of contact between bolt head and joint (it's a ring so a bit confusing to me), L - height of bolt shank/joint, D_hole - diameter of the hole in the joint, A_bolt - cross-sectional area of the bolt.
As you can see, bolt force according to this is around 201 N (100 N for model utilizing symmetry) so way too low. I thought that the problem might be caused by the fact that those equations are meant for tension, not compression but I can't get agreement for tension either. I've also tried applying F_load to the top surface of the bolt head like in the article but it didn't help. There's always such a large difference. I feel that I'm making some silly mistake somewhere here. Do you know what can be the cause of the problem? I will be really grateful for any help.
