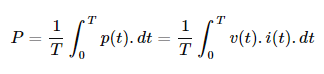I’ve been doing some voltage/current measurements on VFDs and have come across a peculiarity that I do not yet fully understand. The specific VFD I’m working with at the moment is a 2hp drive powered by single-phase (240V), with output to a 3-phase 2hp (230V) motor. I’ve looked at both current and voltage waveforms with a scope, input and output, and am trying to reconcile what seems to be a significantly higher apparent output power than apparent input power (kVA).
Looking at the VFD panel for example, at 3000 rpm I read 185.5 Vrms and 2.1 Arms. This gives an apparent power of 1.732 x 185.5 V x 2.1 A = 674.7 VA. At the drive input, using a Fluke 87V meter, I get 241.2 Vrms and 1.15 Arms. This gives 241.2V x 1.15 A = 277.38 VA. And the operator screen and fan use an additional 162mA that I haven’t subtracted out.
In this case the motor is unloaded, so current is basically the magnetizing current.
I was always under the impression that power in = power out, and that this held for apparent power as well as real power (I thought I had seen this with kVA in transformer calculations, as well as real power for power supplies). It seems that because the VFD is a power converter, somehow it’s not quite that simple. But then how does this play out in the VFD case? And is it only real power in = real power out? What about reactive power?
I appreciate any input.
Looking at the VFD panel for example, at 3000 rpm I read 185.5 Vrms and 2.1 Arms. This gives an apparent power of 1.732 x 185.5 V x 2.1 A = 674.7 VA. At the drive input, using a Fluke 87V meter, I get 241.2 Vrms and 1.15 Arms. This gives 241.2V x 1.15 A = 277.38 VA. And the operator screen and fan use an additional 162mA that I haven’t subtracted out.
In this case the motor is unloaded, so current is basically the magnetizing current.
I was always under the impression that power in = power out, and that this held for apparent power as well as real power (I thought I had seen this with kVA in transformer calculations, as well as real power for power supplies). It seems that because the VFD is a power converter, somehow it’s not quite that simple. But then how does this play out in the VFD case? And is it only real power in = real power out? What about reactive power?
I appreciate any input.