Volume and Wetted Area of a Partially Filled Horizontal (Conical) Frustum?

[Ally0138]

Hi,

Does anyone have formulae for calculating the following:
[ol 1]
[li]The volume of liquid in a partially filled horizontal conical frustum?[/li]
[li]The corresponding 'wetted area' of the frustum?[/li]
[/ol]

Refer to below diagram. I wish to calculate the volume of liquid and the wetted area of the frustum for a liquid height of h within a horizontal frustum of large diameter d1, small diameter d2 and length L.

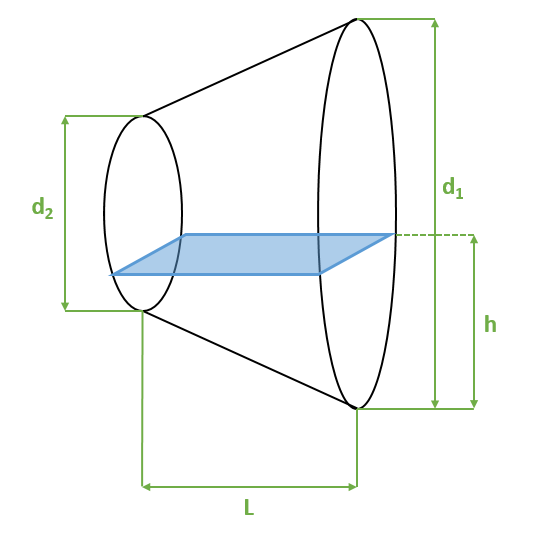
Thanking you in advance for your suggestions.
-Ally-

 

[jari001]

Assuming the diagram is meant to show a right cone -

Volume = (pi*L/3)*(r1^2+r2^2+r1*r2)

Surface area will require knowing the radius at the level of wetting and the height of the liquid, if we call the radius at the level of wetting r2 and the height of the liquid L:
S.A. = pi*(r1+r2)*sqrt((r1-r2)^2+L^2)

 

[bimr]

http://www.analyzemath.com/Geometry_calculators/surface_volume_frustum.html

 

[Ally0138]

Thanks for the response jari,

I don't quite follow your equations, but that may just be because we are using different nomenclature, or maybe my original problem statement wasn't very clear.


Let me attempt to clarify:

The diagram is meant to show a right conical frustum (a parallel truncation of a right cone) shaped vessel oriented horizontally.

The blue parallelogram in my diagram represents the liquid level within this vessel.

I first wish to calculate the volume of liquid in the vessel. The reason I don't follow your first formula is that it doesn't appear to contain a term which represents the height of the liquid (termed 'h' in my diagram).

I'm assuming your nomenclature is as follows:
L = length of the frustrum
r1 = radius of the large end
r2 = radius of the small end

I think the reason I'm having difficulty following your second equation for the wetted area is your choice of nomenclature: I'm not sure I follow what you mean by the 'radius at the level of wetting' and if you are defining L as the height of the liquid, then there's no term in your equation for the length of the vessel.


After having written all of the above, I return to the first thing you said "Assuming the diagram is meant to show..." and am inclined to conclude that you cannot actually see my diagram. I also suspect that your equations are written with a frustum oriented vertically in mind. What if you take the image you have in your mind and turn it 90 degrees onto it's side, what are the equations then?

Best Regards,
-Ally-

 

[Ally0138]

bimr,

Thanks for the response, but the online calculator you linked to doesn't actually give me what I need. The formulae given there are for the total surface area and total volume of a frustum. I need to calculate the liquid volume and wetted area of a partially filled frustum on it's side, as in my original diagram.

Cheers,
-Ally-

 

[bimr]

Think it is all there.

For the wetted area:

Use:

https://www.ck12.org/c/trigonometry/length-of-a-chord/lesson/Length-of-a-Chord-TRIG/

to determine the length of the chord on the circle. Chord length times L = area of rectangle

Here is another one:

http://mathforum.org/library/drmath/view/65656.html

 

[EdStainless]

Ally, you never to analytic geometry?
There are simple math handbooks out there (mine if from the 1930's) that have all of these formula either listed or the derivation framework is set out for you.

= = = = = = = = = = = = = = = = = = = =
P.E. Metallurgy, Plymouth Tube

 

[riddance]

Ally -

Forgive the clunky ASCII formatting of this page, but this is what you are looking for:

http://mathforum.org/library/drmath/view/65656.html

 

[georgeverghese]

Agreed, go through the chapters on derivation of surface area and volumes by using integrals in a calculus textbook - at the outset, it shouldnt take much effort to do this.

 

[jari001]

The mathforum.org link will give you the volume and the surface area will be the derivative of the volume function (since the geometry is symmetric) wrt which dimensions that change as it is filled. Then you will have to add in the surface area of the circular ends of the vessel.