what are the equations of state space on open loop active suspension ?

[DionEng]

Hello

So I need to solve a problem on an active suspension .I dont know how to find the equations of state space on open loop

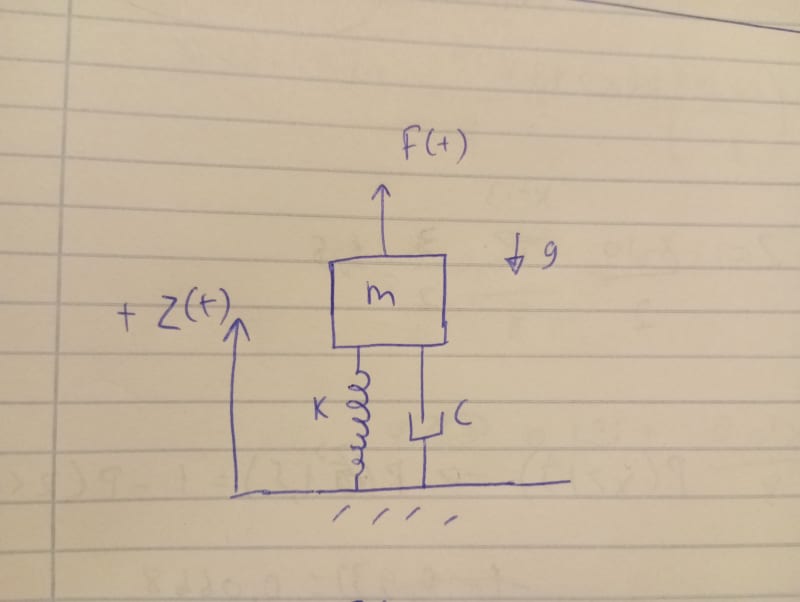
Given information

We apply F(t) force as ypou can see

z(t) is the distance of the upper spring edge from the ground

when spring length (not loaded ) = 1

F (spring) = -kδ^3 (t) δ = displacement of z(t)- z(not loaded)

F ( damper ) = - c dz(t)/dt

 

[rb1957]

what are the forces acting on the mass ?

these force create an acceleration of the mass, hence velocity and displacement.

as I remember this stuff (from 40 years ago) you get a differential equation (xdbldot, xdot, x).

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[DionEng]

F(t) up force

F spring , F damper and weight down force

 

[DionEng]

i am trying to make these x dot dot ,x dot etc but there is δ^3(t) i dont how to make it to x

 

[DionEng]

ma= F(t) - mg - Fspring -Fdamper

 

[GregLocock]

Force in the spring = -k*z
force in the damper =-c*Dz
Net force on mass = -g-k*z+F- c*zD=m*D^2z

Using D notation because this is a typewriter.
There's probably a minus sign or two adrift in that. No D^3


Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[DionEng]

δ is just a symbol δ = ( z-1 )^3 nit derivative
And my problem says that F spring = - kδ^3(t)
I dont know how to turn u it to x dot

 

[Latexman]

ChE here! So, be gentle! Isn’t u (velocity) = x dot = dx/dt

Good Luck,
Latexman

 

[DionEng]

Yes

 

[GregLocock]

Oh, sorry you are using delta to mean dz, I misread your question

Wow, well you cannot easily solve that algebraically. A quadratic rate curve (ie cubic force curve) for a spring is quite a feasible approximation in real life, but to solve it we use numerical solutions.

so -g-k*z*z*z+F- c*Dz=m*D^2z

where k c m and g are constants and D means d/dt

You could try Wolfram Alpha.


Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[Rex Hang]

How can we find the state-space equations for the active suspension system with this information?

 

[GregLocock]

With a cubic spring? Beyond my pay grade.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[DionEng]

Thanks for your replies but I have another question
I want to find the equation of damper ratio ζ>1 but including cubic spring
I know that for linear active (non cubic ) suspension is ζ= (c√m)/(2m√k)
but in my case that i have cubic spring do you have any idea how the equation is