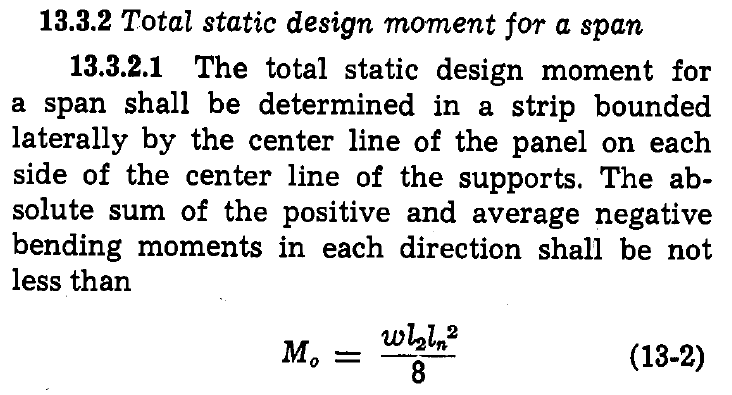
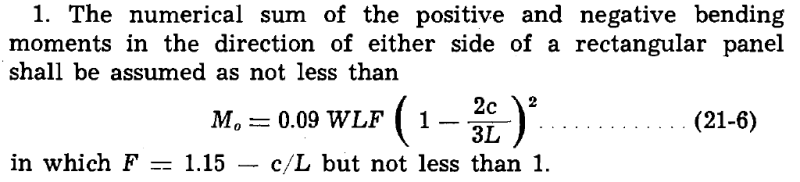JDG3718
Structural
- May 13, 2017
- 25
How the tendon profile is calculated for banded-distributed disposition? In the following figure why is the tendons profile one in the top fiber and the second in the bottom fiber? If the location is at the middle of the slab why do we place them opposite to each other doesn't that cancel the effect of the lower tendon?


![[thumbsup2] [thumbsup2] [thumbsup2]](/data/assets/smilies/thumbsup2.gif)