Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations cowski on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
What is the maximum acceleration in horizontal direction without spilling water from the glass 4
- Thread starter hungy_kid
- Start date
goutam_freelance
Mechanical
Initial volume=Volume below lowest point on water surface+1/2(Full glass volume-volume below lowest water surface).
Water surface divides the volume above lowest surface point in 2 equal halves.
Engineers, think what we have done to the environment !
Water surface divides the volume above lowest surface point in 2 equal halves.
Engineers, think what we have done to the environment !
goutam_freelance
Mechanical
As I told before the concept needs to be checked. I shall check again.
Engineers, think what we have done to the environment !
Engineers, think what we have done to the environment !
I think the glass will fall over before the nominal water level sloshes. I don't see a weight/CG for the material that forms the cup, so there's no way to tell where the water is to begin with.
The simple method first-order acceleration test is to put a glass on a slope of the same material as the conveyor belt and tilt it until it falls over.
The simple method first-order acceleration test is to put a glass on a slope of the same material as the conveyor belt and tilt it until it falls over.
I think you're right 3DD. there is 124mm of water, so the CG is somewhere north of 62mm, and the base is radius of 25mm. so a combined acceleration vector of nearly 45deg (10m/s2 down and 10 m/s2 to the right) would be considerably outside the base ...
another day in paradise, or is paradise one day closer ?
another day in paradise, or is paradise one day closer ?
goutam_freelance
Mechanical
On further thought I found that the procedure given by me is approximately true, since the glass side angle is small( 9 deg approx). The formula is correct if the glass is perfectly cylindrical. But till now I am unable to find a formula for division of cone volume by a diagonal plane. Hope somebody here will be able to help.
Engineers, think what we have done to the environment !
Engineers, think what we have done to the environment !
The fun thing about a diagonal cut on a cone is it forms an ellipse. While there is a formula to calculate the area of an ellipse, AFAIK there is no formula to exactly calculate the length of the ellipse perimeter except for a circle.
With a cylinder this is a trivial calculation; on a cone, not so much.
With a cylinder this is a trivial calculation; on a cone, not so much.
- Thread starter
- #27
- Thread starter
- #28
Yet again my not asking for a photograph leads to misunderstanding.
Water density doesn't matter if all you are concerned about is where the liquid reaches the lip of the cup. All liquids will have a surface normal to the local acceleration.
So, since those dimensions must be the inside of the cup you should be able tip the cup so the water just reaches the lip and the tangent of that angle is the ratio of horizontal acceleration to vertical acceleration that will reach that point.
Water density doesn't matter if all you are concerned about is where the liquid reaches the lip of the cup. All liquids will have a surface normal to the local acceleration.
So, since those dimensions must be the inside of the cup you should be able tip the cup so the water just reaches the lip and the tangent of that angle is the ratio of horizontal acceleration to vertical acceleration that will reach that point.
- Thread starter
- #30
Yeah, I realized that after engaging with you guys and reading up some more on that. But I am still curious how to calculate it from theoretical point of view. Goutam_freelance seems like is onto something, but I am not really sure how he came up with that equation where he finds tan(alpa). Years of not doing much hand calculations and relying on softwares must have dumbed me down. Are you able to see what he has done there?
rather than looking at the ideal case of a steady acceleration and setting the water surface to the lip of the cup (and yes we haven't solved the volume of a cone cut by an inclined plane ... maybe do it in CAD ?) ...
I think the critical case was identified by 3DDave ... when does the acceleration vector become unstable ... move beyond the footprint of the cup. If we have an initial water level of 124mm then the CG height is roughly 62mm, and the base radius is 25mm. so an acceleration of 25/62, approx .5g, would be close to tip over the cup. Yes, I know it'll be more than that as we need the contact pressure at the other side of the cup to go to zero (from the static pressure). But this seems to be much lower than the estimates of the water surface (which seem to be about 1g).
another day in paradise, or is paradise one day closer ?
I think the critical case was identified by 3DDave ... when does the acceleration vector become unstable ... move beyond the footprint of the cup. If we have an initial water level of 124mm then the CG height is roughly 62mm, and the base radius is 25mm. so an acceleration of 25/62, approx .5g, would be close to tip over the cup. Yes, I know it'll be more than that as we need the contact pressure at the other side of the cup to go to zero (from the static pressure). But this seems to be much lower than the estimates of the water surface (which seem to be about 1g).
another day in paradise, or is paradise one day closer ?
This is pretty simple to set up in CAD.
Simply vary the angle until the volume becomes 500cc (same as 0.5kg of water)
Angle is apx 28.5 degrees
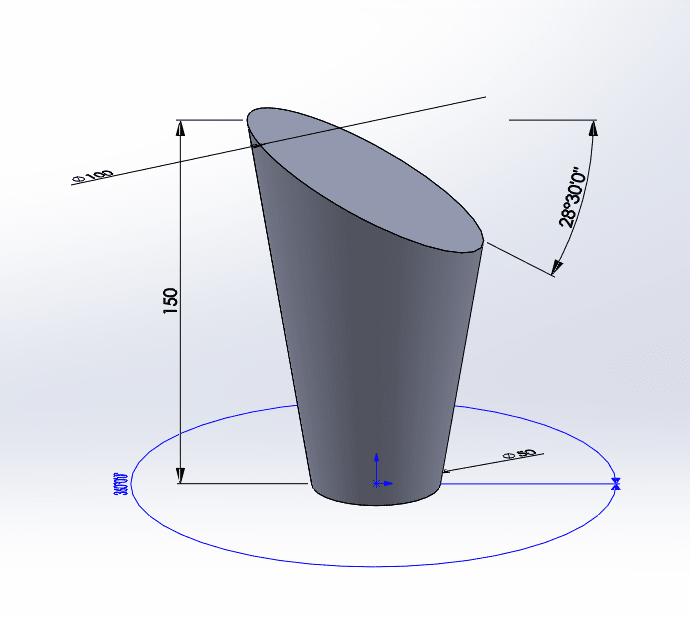
Now find the CG (another CAD feature) and drop a line perpendicular to the fluid surface.
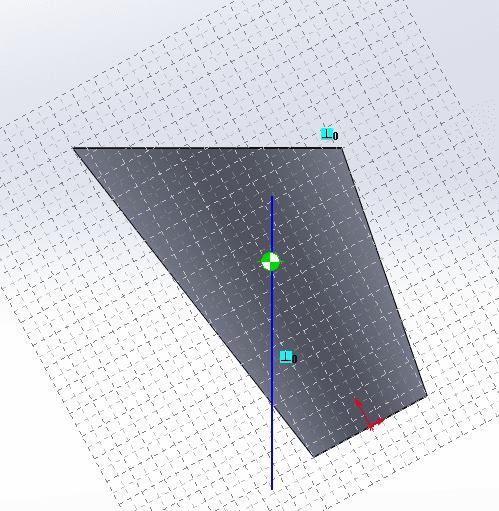
CG line is significantly to the left of the cup edge, therefore the cup will tip over before it spills. However, if the cup were somehow glued to the conveyor, the acceleration is tan(28.5)g
Simply vary the angle until the volume becomes 500cc (same as 0.5kg of water)
Angle is apx 28.5 degrees
Now find the CG (another CAD feature) and drop a line perpendicular to the fluid surface.
CG line is significantly to the left of the cup edge, therefore the cup will tip over before it spills. However, if the cup were somehow glued to the conveyor, the acceleration is tan(28.5)g
goutam_freelance
Mechanical
@hungry_kid
Lately I have some free time so I decided to' Go back to School'.
The following are from Schaum's Outlines-Fluid Mechanics:
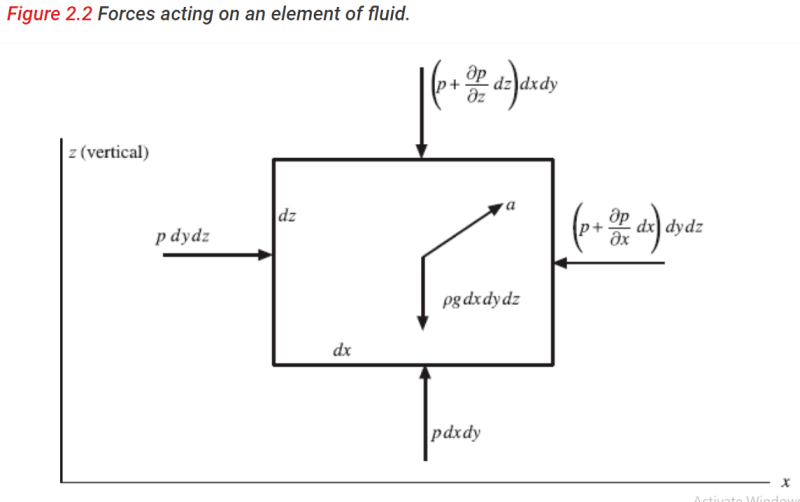
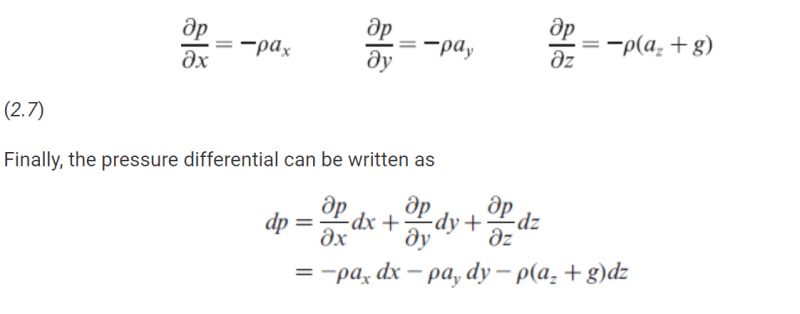
Now refer the original figure posted by me.
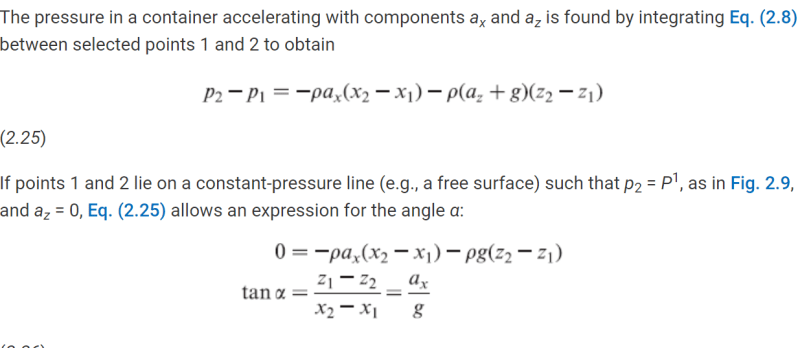
@handleman, thank you for the info. Yes it can be done with CAD. But I was looking for a formula to put it into an equation.
Engineers, think what we have done to the environment !
Lately I have some free time so I decided to' Go back to School'.
The following are from Schaum's Outlines-Fluid Mechanics:
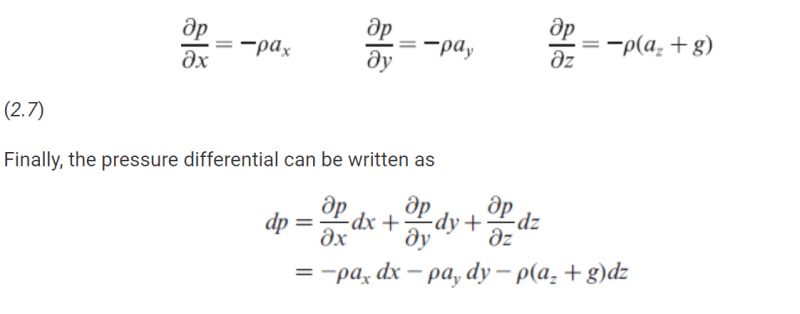
Now refer the original figure posted by me.
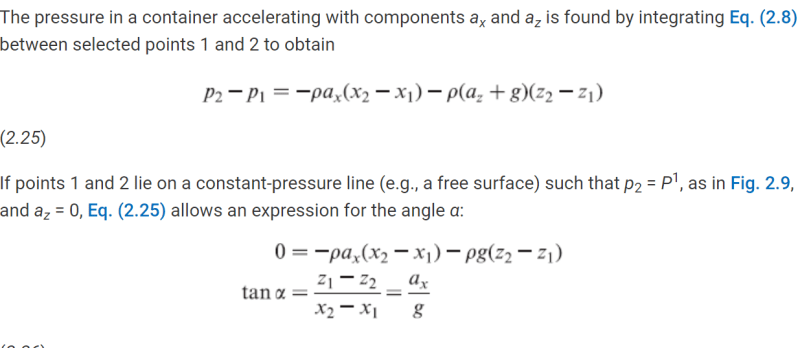
@handleman, thank you for the info. Yes it can be done with CAD. But I was looking for a formula to put it into an equation.
Engineers, think what we have done to the environment !
-
1
- #34
Formula for the volume of a cone truncated at an angle is here:
This problem could be solved geometrically/algebraically. The water surface should remain approximately normal to the resultant acceleration vector (gravity + local acceleration). Setting up a system of equations should make this problem trivial for analytical solution. I'd set it up as follows: volume of empty glass - volume of air in glass (inverse of liquid). The volume of air is the integral of a set of ellipses through an angle which describes the surface of the liquid. The angle (which is the upper bound of the integral) would be normal to the resultant acceleration vector. The rest is algebra. In this way one could develop a set of equations useful for resolving with different sized containers and different amount of liquid.
-
1
- #36
goutam_freelance
Mechanical
@handleman, thank you. The formula you gave was very useful. I have redone the calculation. The angle and hence acceleration tallies with CAD output.
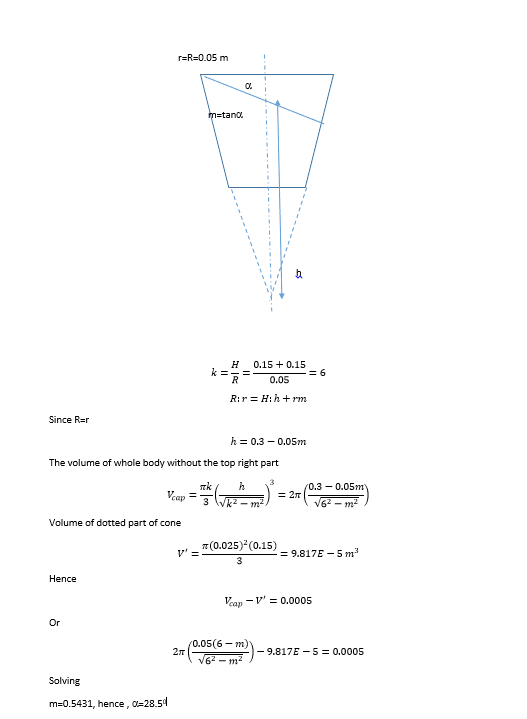
The numerical solution was done in Matlab using fzero() function.
Engineers, think what we have done to the environment !
The numerical solution was done in Matlab using fzero() function.
Engineers, think what we have done to the environment !
- Thread starter
- #37
I'd take your 'glass' to anywhere that has a conveyor driven by a VFD (lots of places use them) and just test it. You may see things and results that you haven't even considered and you will know for sure.
Keith Cress
kcress -
Keith Cress
kcress -
I am not convinced that a static geometric model is representative of the water sloshing, especially without knowing the force-vs-time for the conveyor start and stop events. It might make a difference if the spillage is defined as one drop or some percentage of the volume in the cup. Some testing could provide the solution or at least validate the model. I am with itsmoked on this one.
Walt
Walt
1.[ ] Use ElectricPete's 14Jan21@14:53 approach to find the surface's "steady state" slope under a constant acceleration.
2.[ ] Double that slope to get a reasonably accurate estimate of the maximum transient slope that would be caused if the acceleration came on instantaneously.
[Correction/edit at 20:30 18Jan21 UTC.][ ] It is, of course, the tan() of the slope that should be doubled.
2.[ ] Double that slope to get a reasonably accurate estimate of the maximum transient slope that would be caused if the acceleration came on instantaneously.
[Correction/edit at 20:30 18Jan21 UTC.][ ] It is, of course, the tan() of the slope that should be doubled.
- Status
Similar threads
- Locked
- Question
- Locked
- Question
- Locked
- Question
- Locked
- Question
