CorporalToe
Civil/Environmental
Hello I was doing a question in order to prep for the PE exam and I ran into this problem which I got wrong.
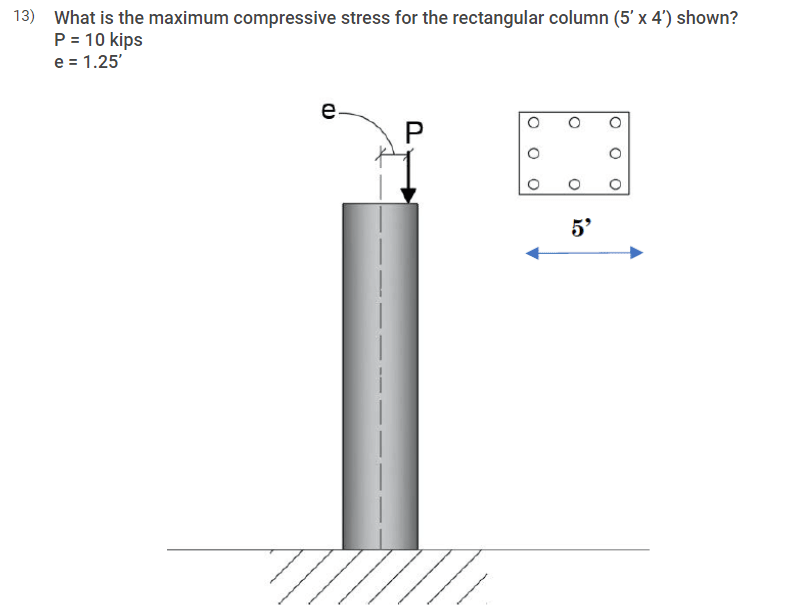
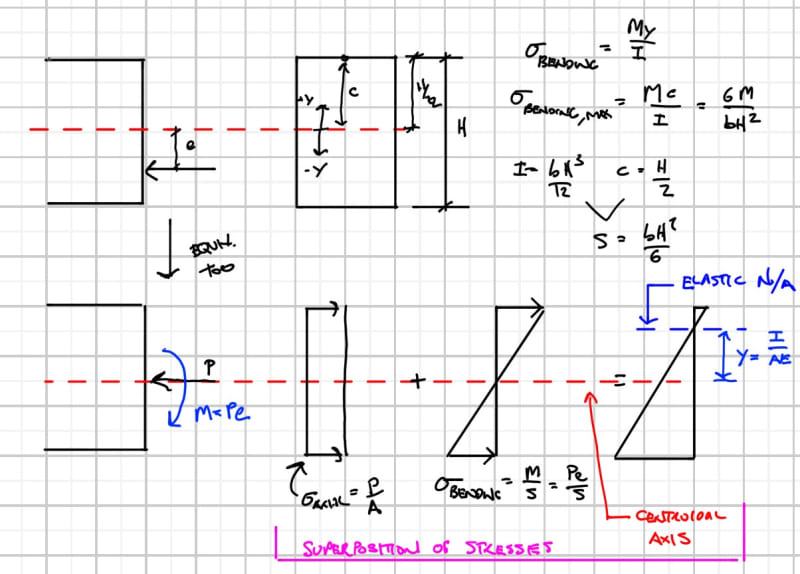
In this question since the cross section is being loaded axially plus a moment due to the eccentricity, that the neutral axis will shift from the centroid location. However in the solution they do not shift the NA why is this?
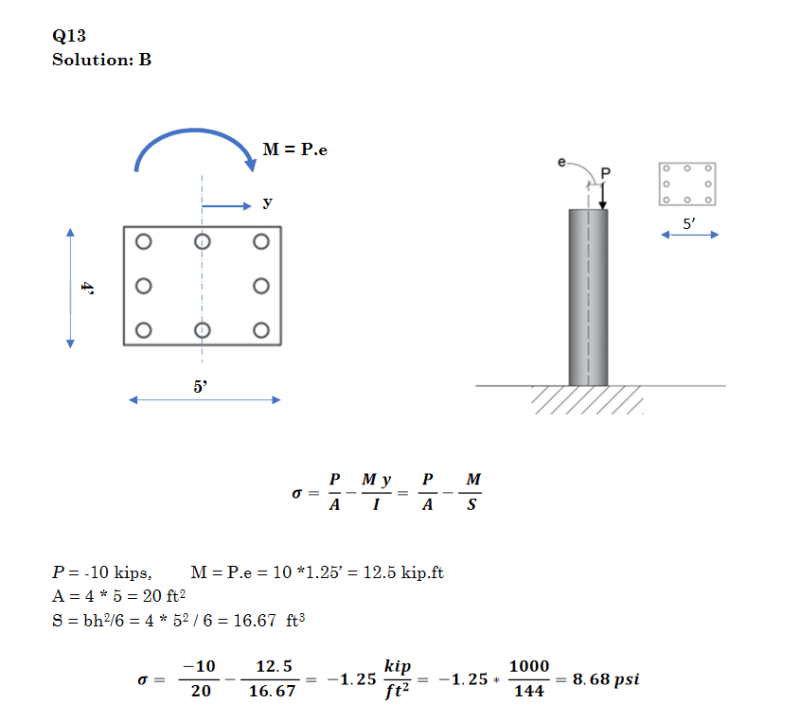

In this question since the cross section is being loaded axially plus a moment due to the eccentricity, that the neutral axis will shift from the centroid location. However in the solution they do not shift the NA why is this?