When a Guyan reduction is applied to a finite element model and reduced to a statically determinate number of degrees of freedom (1 node/6dof), why does the reduced stiffness matrix become zero? I've been trying to wrap my head around this all day, and I understand the intuition behind it. The definition of a statically determinate system is that the system's equilibrium equations are fully sufficient to describe its behavior; therefore, the stiffness matrix is simply redundant and not necessary to define the system's behavior. Additionally, if you displace that one node, everything should move rigidly and forces should be zero. Henece, the K matrix must be zero. That all makes sense. But I don't understand how the math works that it comes out to be zero.
K_reduced =
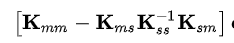
So, in this case, the left (boundary/preserved) and right (internal/omitted) stiffness terms are exact. Thus, K_reduced = 0.
Working out the math to get the result isn't difficult, but why does K_mm = k_ms*K_ss^-1*K_sm only when the size of K_mm is statically deteremiant is puzzling me. I would appreicate any insights you guys could provide. Thanks
K_reduced =
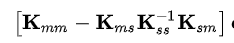
So, in this case, the left (boundary/preserved) and right (internal/omitted) stiffness terms are exact. Thus, K_reduced = 0.
Working out the math to get the result isn't difficult, but why does K_mm = k_ms*K_ss^-1*K_sm only when the size of K_mm is statically deteremiant is puzzling me. I would appreicate any insights you guys could provide. Thanks
