RBstructural
Structural
- Aug 18, 2021
- 3
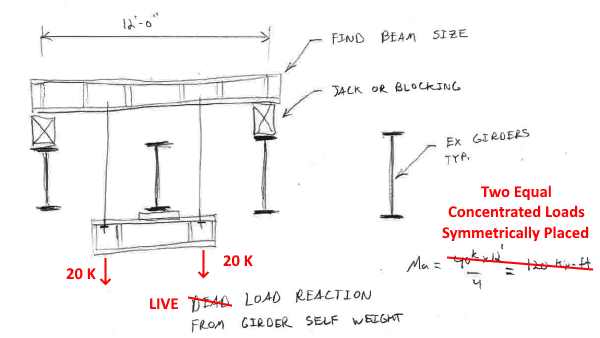
I work for a steel erector and I frequently see wide flange beams in the shop or yard sitting simply supported on timber blocking with no top flange bracing. I am wondering if there is a way to quantify the bending strength in this condition. In many cases, falsework designs or initially erected conditions are similar and I feel inclined to provide tie downs or temporary bracing to the top flange at supports where I am not sure how to determine the capacity if I feel it does not meet AISC Appendix 6 and AISC F1(2) requirements for restraining points of support against rotation about their longitudinal axis. Having a way to quantify the strength in a beam where it is supported on blocking at its bottom flange with nothing restraining its top flange could be very advantageous. I'm wondering if anyone can provide a reference or shed some light on this scenario.

![[idea] [idea] [idea]](/data/assets/smilies/idea.gif)