X-Braces with Central Node Moved Upward - 6

[Cpw628]

I came across the article "Evolution of the Braced Tube" by Structure Magazine that shows the 800 Fulton Market in Chicago as having an X brace with the center of the X shifted up. The article states that when the members are deflection controlled this is more efficient, but doesn't get into why. I made a model and included some screenshots from it, but am having a hard time understanding why and what shifting the node does. I'd also imagine that this significantly reduces the ductility of the structure if one of those braces buckle.

See page 46 of the June 2024 edition of the Structure Magazine.
Link

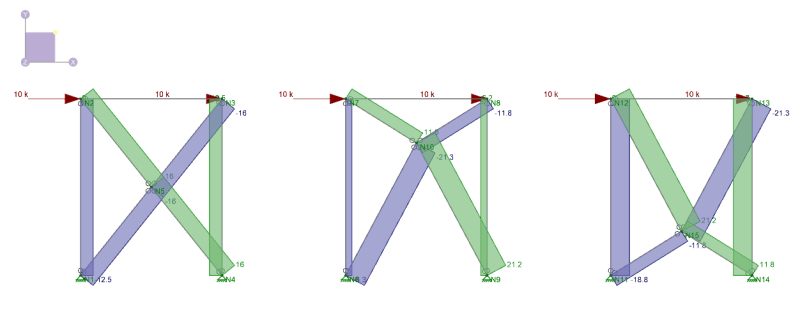
Axial forces in braces:

Deflections in all 3 braces at the top left corner of brace:

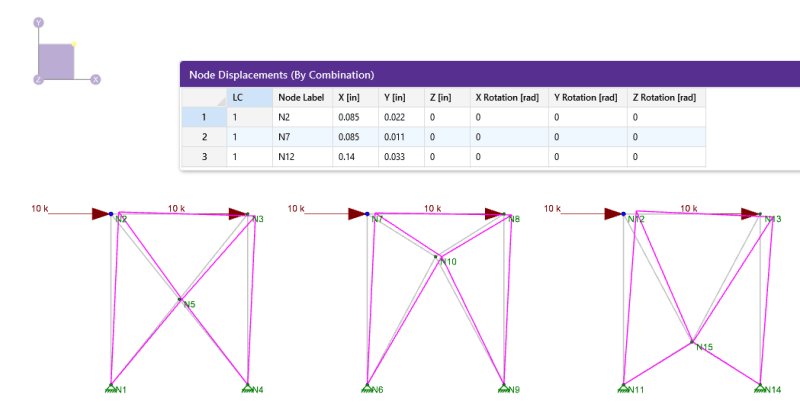
Image of 800 Fulton Market:

 

[canwesteng]

If you go through the princeton paper and go through fig 6 and equations 16/17, I think it's pretty in line my sketch/understanding. They've just crunched all the numbers to actually optimize it for deflection

 

[BulbTheBuilder]

Deker's post highlights the concepts. The concept used here is topology optimization and I am guessing truss optimization was utilized. Basically, we take a solid member, apply the loads, and set a number of constraints (strain; deflection limit, stress, etc) with an object function.

Members with less strain or stress are removed from solids as they are inefficient. There is a penalization factor of 3 typically used as a results there's still some "redundancy" in the system after portions have been removed the solid. Elements (meshed) with higher stresses are maintained. During the iterative process, materials are technically redistributed based on the stresses in the body after certain inefficient elements have been removed.

Topology Optimization: Theory, Methods, and Applications by Martin P. Bendsøe, O. Sigmund, Martin Philip Bendsoe, et al. is a great book on this topic.