Continue to Site

Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in
  • Congratulations waross on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!

Total friction loss through parallel streamlines

Status
Not open for further replies.
carledritten

carledritten

Petroleum
Feb 15, 2016
6
Hi,

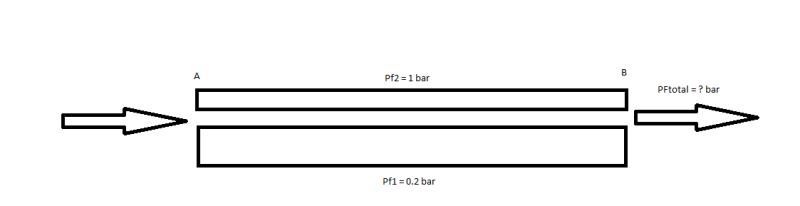
Lets say I have two parallel streamlines for gas between point A and point B, and two parallel streamlines for liquid between point A and point B. Further, I know the friction losses for all 4 streamlines. Then, how can I calculate the total friction loss for the gas, and the total friction loss for the liquid?

PS I suspect that parallel electrical circuit laws can be used somehow [1/R[sub]T[/sub] = Σ(1/R[sub]i[/sub]) or 1/√R[sub]T[/sub]=Σ(1/√R[sub]i[/sub])]

\Carl
 
Replies continue below

Recommended for you

Sort by date Sort by votes
Since in the real world, there is no way to know the pressure drop down a stream line, I have to say that homework problems are not allowed at eng-tips.com.

David Simpson, PE
MuleShoe Engineering

In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual. Galileo Galilei, Italian Physicist
 
Upvote 0 Downvote
This is the real world, and no, it is not a "homework problem".

I have roughly estimated the frictional losses based on geometry and velocities. The velocities are "first guesses" in the Bernoulli equation, and I will use iteration to find the end solution. But before I can do that, I need to combine the two frictional streamlines for the gas and liquid phase.

Hope you guys can help me out.

\Carl
 
Upvote 0 Downvote
Your question is not clear. If you already know the friction loss in each of the lines from A to B what else is there to know?

Katmar Software - AioFlo Pipe Hydraulics

"An undefined problem has an infinite number of solutions"
 
Upvote 0 Downvote
I'm asking for the total friction loss for each phase. If all the streamlines were in series, I could simply add them together and have the total friction loss. But they are flowing in parallel, and therefore I'm not sure how to do it. Can it be done by using the circuit laws as I mentioned earlier, or do I need to take another approach?
 
Upvote 0 Downvote
Drawing this would be a good plan.

The only thing you actually know is the pressure drop between your points A and B is the same for each pipe. I hope by streamline you actually mean pipe. Please confirm or otherwise this post is talking rubbish.

You say parallel, but are the two pipes for each fluid the same size?

For any given pipe size and lengthy, resistance to flow is more or less proportional to the square of the velocity.

Energy loss is head loss times flew times density.

Is this what you want to find?

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
 
Upvote 0 Downvote
Yes, I'm talking about pipes. And no, the pipes are not the same size.

I'm asking for a formula to calculate total friction loss for parallel pipes.

I have tried to illustrate it in the picture. Upstream point A and downstream point B, there is a common pipe.

friction_loss_z0gmti.png
 
Upvote 0 Downvote
If the two pipes come out of a common header and go back into a common header, then the dP HAS TO BE THE SAME in the two pipes. If you know dP, then you can calculate the relative flow rates (I'd use something with explicit friction factors instead of the shortcut programs). Total friction drop is what you measure in the upstream and downstream headers. I'm not seeing this problem as anything but either impossible or trivial. The volume flow rate in the two pipes is unlikely to be the ratio of the flow areas, just because no two pipes have identical roughness.

David Simpson, PE
MuleShoe Engineering

In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual. Galileo Galilei, Italian Physicist
 
Upvote 0 Downvote
Would these two phases be mixed in order to determine an equivalency value in pressure drop, otherwise what's the point?
 
Upvote 0 Downvote
chicopee: Yes, the phases will eventually be mixed. The equivalence pressure drop for the phases is the key. But to find this common value, the total friction for each phase must be defined.

dicksewerrat: Taking one of the pipes out of service is not an option.
 
Upvote 0 Downvote
Unless point a and point b repent some very large reservoirs, a complication is that your flow has an impact on upstream and downstream flow.

What do you mean by total friction drop? Pressure drop is often the same thing.

Your first point is the fact that your pressure drops in all the pipes is the same. Your variables are many, but flowrate is the first one to resolve.

Depending how long these pipes are the density of your gas might change from one end to the other.

You really nerd to start putting some dimensions to this to have any chance of solving it. I don't think threes any easy formulae.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
 
Upvote 0 Downvote
Well, your work is going to be cut out for you since mixing a gas with a liquid can produce several flow regimes such as annular flow, plug flow, bubble flow etc... There is no short cut on this subject, therefore, I would suggest that you read related literature on this subject. If I remember correctly, Perry chemical engineering handbook is a starting point. Another reference is by GF Hewitt on two phase flows. This subject has been extensively researched by others so do a web search. By the way, your example of two pipes in series with each pipe carrying each phase will not really work the way you think unless you have something like a plug preventing the two phases from mixing.
 
Upvote 0 Downvote
Just thinking about your problem, do a search on air lift pumps as this field of research goes into the different flow regimes, pressure drops, etc...
 
Upvote 0 Downvote
chicopee:

I'm thinking the two upper pipes (Are the upper two vent pipes of some kind - connected somehow on both ends to liquid service pipes below? ) are going to start vaporizing first, and will be probably mostly gas at saturation conditions for most of the length. If they drain - maybe back to the first reservoir - then they'd be a mix of vapor on the bottom flowing with gravity, and vapor on top flowing with pressure. The condensate could be pushed along though - depends if the upper pipe would ever "plug up" with too much liquid to let the gas go by. Depends too on delta P, and if my guess about drain direction is right.

Lower pipe seems a mix of vapor in the upper pipe and liquid in the lower, unless the pump suction from reservoir 1 is always below the condensate level. Then you'd only have flashing problem down low. Same guess as above: I'd need to a complete 3D model or drawing to begin doing anything but guessing.
 
Upvote 0 Downvote
I appreciate all the inputs, and it is more challenging than expected.

What about single phase flow through the pipes? Is there any way to determine the total friction loss with a simpler approach?
 
Upvote 0 Downvote
Personally I'm still trying to work out what you mean by "total friction loss".

If you mean the energy expended, then you can use the pump hydraulic power equation

P = Q x Dens x g x h / 3.6x10^6
P - kW
Q- m3/hr
Dens = density in kg/m3
g = 9.81
h hydraulic head loss in m of fluid (you can get this from your pressure drop)

For the same pressure drop, flow through different size pipes is around (d/D)^2

Look at this threads and scroll down to the post by Katmar


Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
 
Upvote 0 Downvote
If the pipes are connected at A and at B, the pressures are equal at A, and also at B, so the drops must be equal, no?
 
Upvote 0 Downvote
To racookpe1978- obviously, it all depends on the temperature and pressure of the fluids for vaporization to take.
To TenPenny - we all agree with what you are saying, however, the subtle intent of the original OP is to mix two phases presumably flowing at different rates and pressures.
 
Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

VFreshEngineer
  • Locked
  • Question
Head loss through air intake duct piping
Replies
2
Views
190
mrev23
mrev23
PD2
  • Locked
  • Question
Friction factor question 8
Replies
19
Views
297
fel3
fel3
Mark_B
  • Question
Calculating flow through (heating water) coil given only pressure drop and coil measurements 1
Replies
16
Views
8K
btrueblood
btrueblood
timsch
  • Question
Trying to determine airflow through a pipe when vacuum is applied 1
2
Replies
31
Views
6K
timsch
timsch
S.G
  • Locked
  • Question
Minimum crossing/parallel clearance between direct buried cables (33KV power cable) and gas pipeline
Replies
3
Views
207
LittleInch
LittleInch

Part and Inventory Search

Sponsor

Back
Top Bottom