carledritten
Petroleum
- Feb 15, 2016
- 6
Hi,
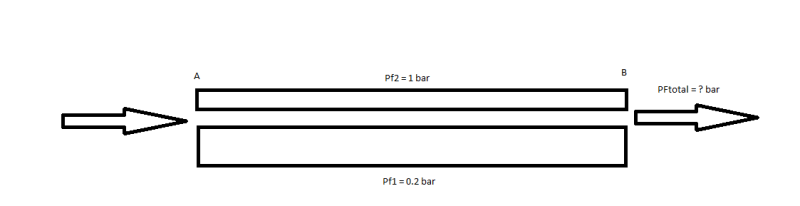
Lets say I have two parallel streamlines for gas between point A and point B, and two parallel streamlines for liquid between point A and point B. Further, I know the friction losses for all 4 streamlines. Then, how can I calculate the total friction loss for the gas, and the total friction loss for the liquid?
PS I suspect that parallel electrical circuit laws can be used somehow [1/RT = Σ(1/Ri) or 1/√RT=Σ(1/√Ri)]
\Carl
Lets say I have two parallel streamlines for gas between point A and point B, and two parallel streamlines for liquid between point A and point B. Further, I know the friction losses for all 4 streamlines. Then, how can I calculate the total friction loss for the gas, and the total friction loss for the liquid?
PS I suspect that parallel electrical circuit laws can be used somehow [1/RT = Σ(1/Ri) or 1/√RT=Σ(1/√Ri)]
\Carl