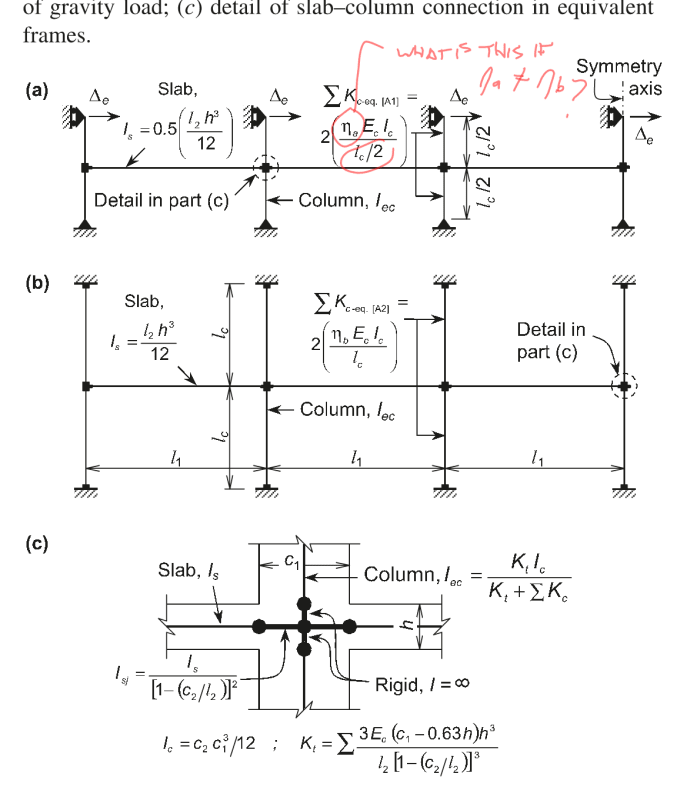
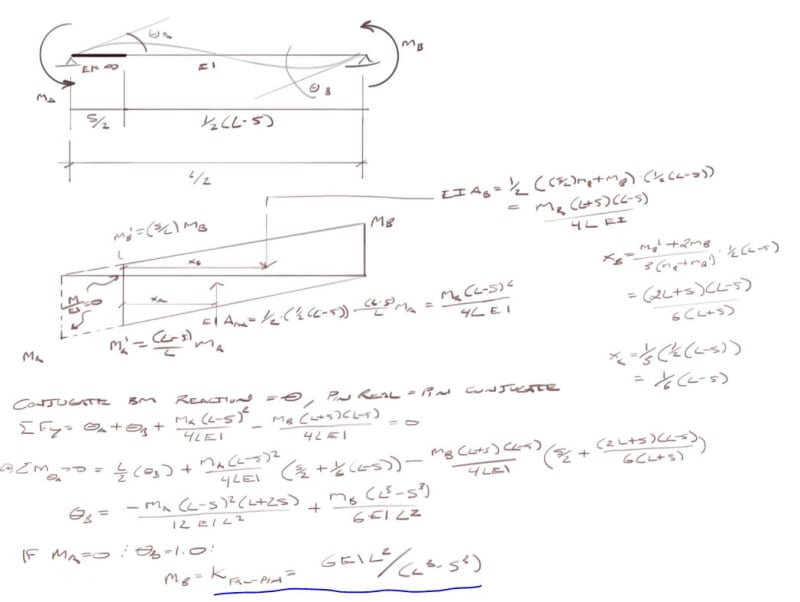
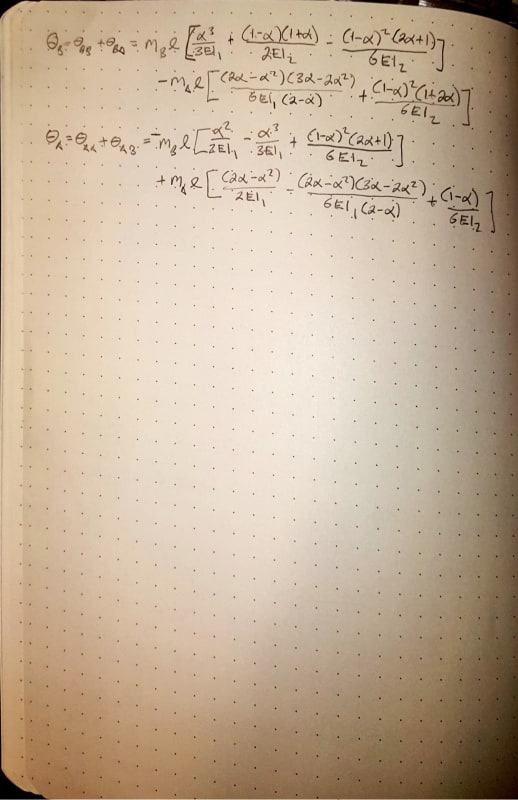So I was working through trying to teach myself the equivalent frame method from ACI318, specifically looking at some of the examples in ACI421.2 related to flat plates. But for the life of me I'm not getting the same answer for Example 1 (see attachment below). In particular my main question is with calculating the equivalent column stiffness, does anyone agree with the ACI value, and if so where did I go wrong? I wonder if someone can take a look and see if they agree with me or if I've made some dumb mistake somewhere.
I will note that doing the analysis talked about for the unbalanced moment based on a accommodating a 0.75" drift gives me the exact same moment they get, so it leads me to believe I've made some mistake somewhere. But then I've reviewed a number of other examples I found online and in PCA notes and seem to be following the same procedure as far as I can tell with respect to undertaking an equivalent frame analysis.
Next question for anyone familiar with ACI421.2, when doing the lateral analysis to determine the out of balance moment, just wanted to confirm whether the bit of slab modeled inside the column also has the 0.25-0.5 stiffness reduction applied as per the slab span outside of the column? EDIT the reason I ask this is initially I applied the reduction tot his region also, but the only way I can get the same moment as the ACI example is to only apply the 0.5 reduction beyond the column area and use full I_s in the column region
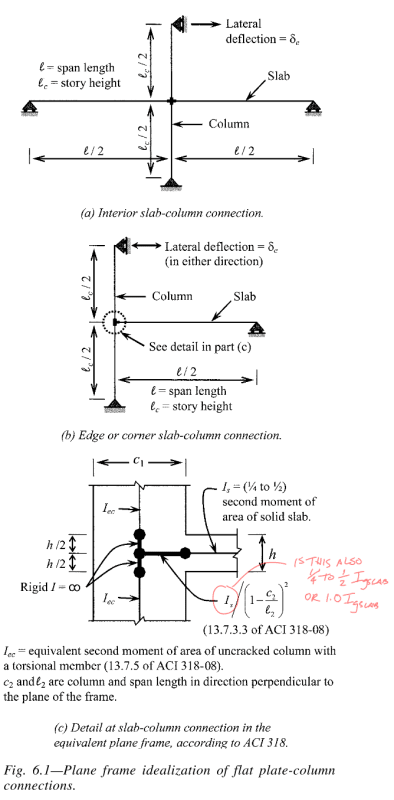
Thirdly, in the example attached, one thing that makes no sense to me given I don't practice in the states and are not really familiar with the inner workings of US loadings codes, is that they are checking this column/slab connection for 2% drift but then they come up with 0.75" drift when the elastic drift or compatibility drift this connection will see will be 2% x storey height of 12' = 2.88" drift (i.e. same as shear walls in building). Why is the drift being reduced, seems illogical to me if the floor system is going along for the ride to 2% total drift as stated? For example they are stating at 0.75" drift these upper limits are not applying, but they sure as eggs will if you push it to 2.88" drift...
Thanks for any input!
I will note that doing the analysis talked about for the unbalanced moment based on a accommodating a 0.75" drift gives me the exact same moment they get, so it leads me to believe I've made some mistake somewhere. But then I've reviewed a number of other examples I found online and in PCA notes and seem to be following the same procedure as far as I can tell with respect to undertaking an equivalent frame analysis.
Next question for anyone familiar with ACI421.2, when doing the lateral analysis to determine the out of balance moment, just wanted to confirm whether the bit of slab modeled inside the column also has the 0.25-0.5 stiffness reduction applied as per the slab span outside of the column? EDIT the reason I ask this is initially I applied the reduction tot his region also, but the only way I can get the same moment as the ACI example is to only apply the 0.5 reduction beyond the column area and use full I_s in the column region

Thirdly, in the example attached, one thing that makes no sense to me given I don't practice in the states and are not really familiar with the inner workings of US loadings codes, is that they are checking this column/slab connection for 2% drift but then they come up with 0.75" drift when the elastic drift or compatibility drift this connection will see will be 2% x storey height of 12' = 2.88" drift (i.e. same as shear walls in building). Why is the drift being reduced, seems illogical to me if the floor system is going along for the ride to 2% total drift as stated? For example they are stating at 0.75" drift these upper limits are not applying, but they sure as eggs will if you push it to 2.88" drift...
Thanks for any input!