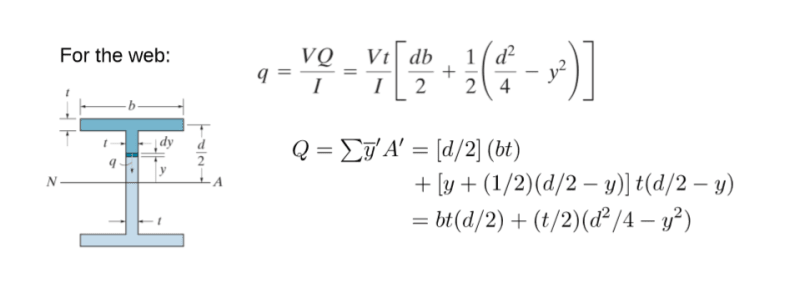Hi All,
I have come across a situation where channels are welded to the web of the wide flange to reinforce the existing beam. This detail is on existing drawings and its a building that was built in 1980's. The beam is a roof purlin supporting deck and snow. Seems like it was reinforced as it was over-stressed by 15%. Maybe beam was reinforced as shown below because of site condition. I cant say why exactly.
I am re-evaluating the capacity of the composite section and I need some inputs. All members are A36 steel. I am using ASIC 360-13th edition and seems like the sections are compact. I am using section F2 to evaluate the capacity and there is around 30% increase in capacity with channel reinforcement compared to W8X10 steel alone. Is using section F2 the correct way of doing it? Also how do I calculate the weld required between the channel and the wide flange? As the CG of channel and the composite section are at the same location the equation VQ/I goes to zero.
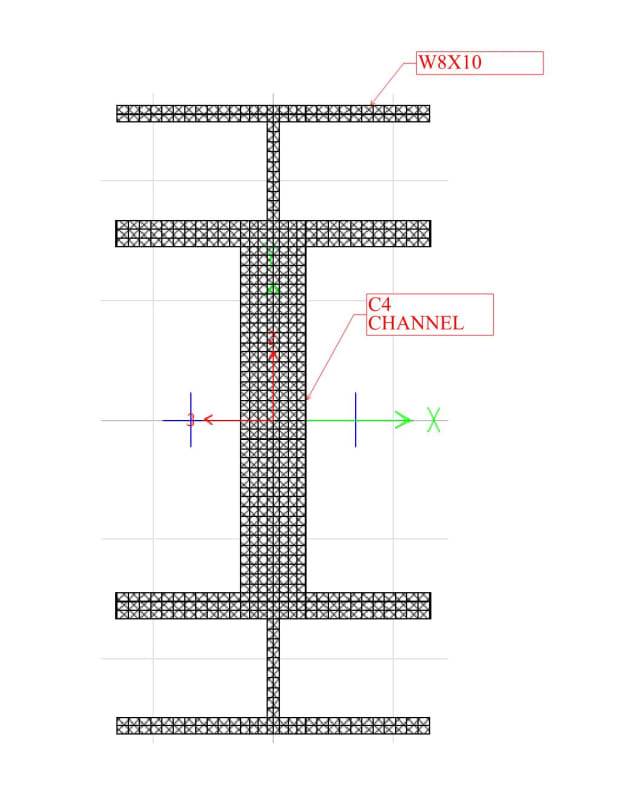
I have come across a situation where channels are welded to the web of the wide flange to reinforce the existing beam. This detail is on existing drawings and its a building that was built in 1980's. The beam is a roof purlin supporting deck and snow. Seems like it was reinforced as it was over-stressed by 15%. Maybe beam was reinforced as shown below because of site condition. I cant say why exactly.
I am re-evaluating the capacity of the composite section and I need some inputs. All members are A36 steel. I am using ASIC 360-13th edition and seems like the sections are compact. I am using section F2 to evaluate the capacity and there is around 30% increase in capacity with channel reinforcement compared to W8X10 steel alone. Is using section F2 the correct way of doing it? Also how do I calculate the weld required between the channel and the wide flange? As the CG of channel and the composite section are at the same location the equation VQ/I goes to zero.


![[idea] [idea] [idea]](/data/assets/smilies/idea.gif)