-
1
- #1
Johns20188
Structural
- Jan 26, 2015
- 14
I've been keeping up with the thread below:
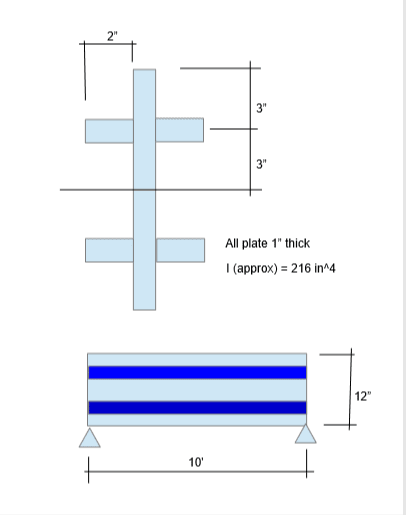
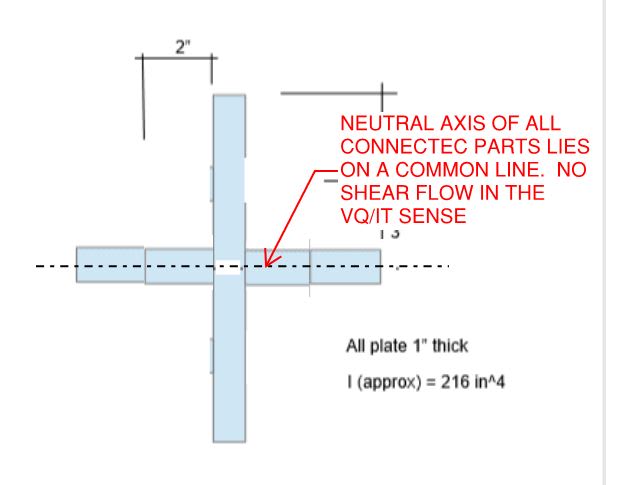
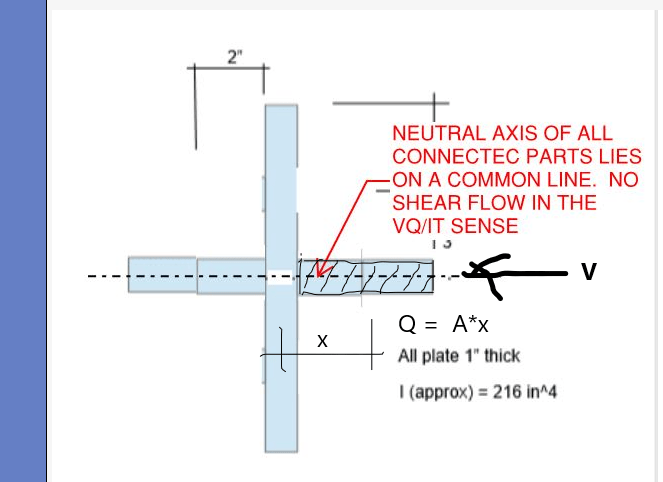
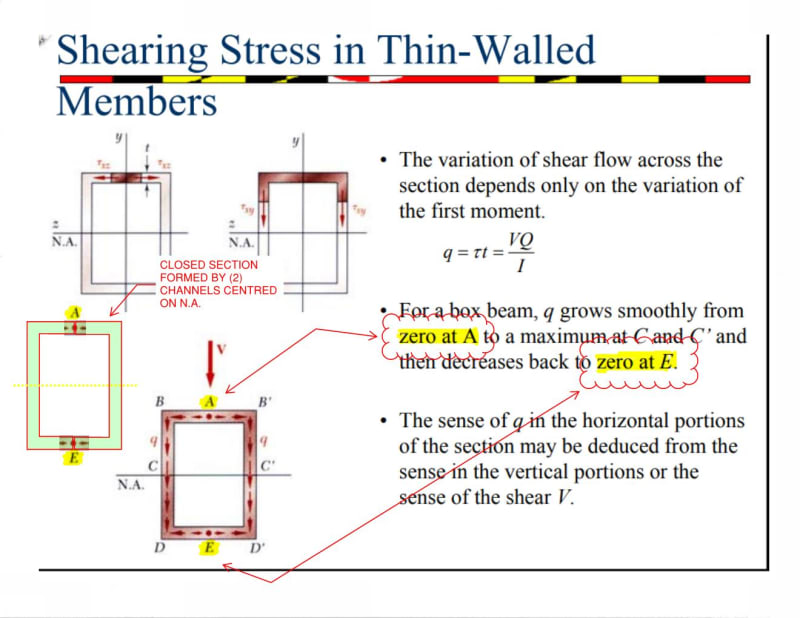
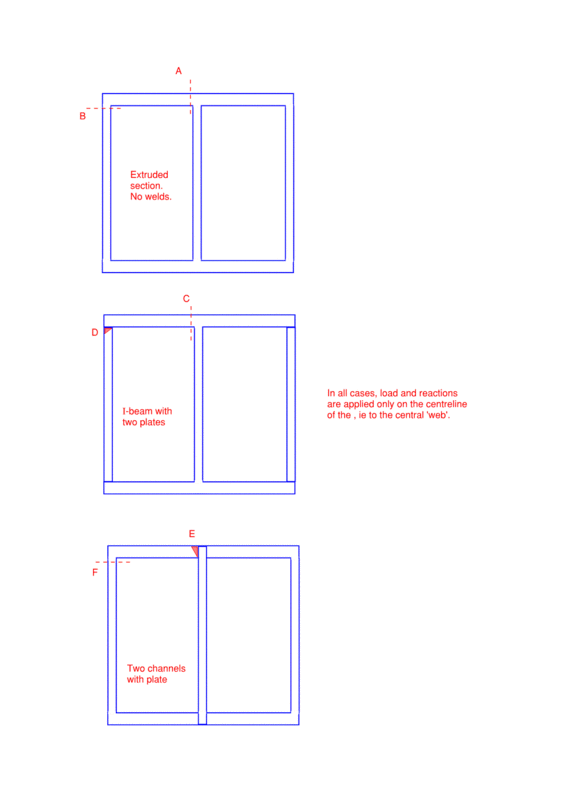
There's a lot of great discussion regarding shear flow of members that share the same Neutral Axis. From the thread responses, it seems that there is no shear flow between the members that share a neutral axis.
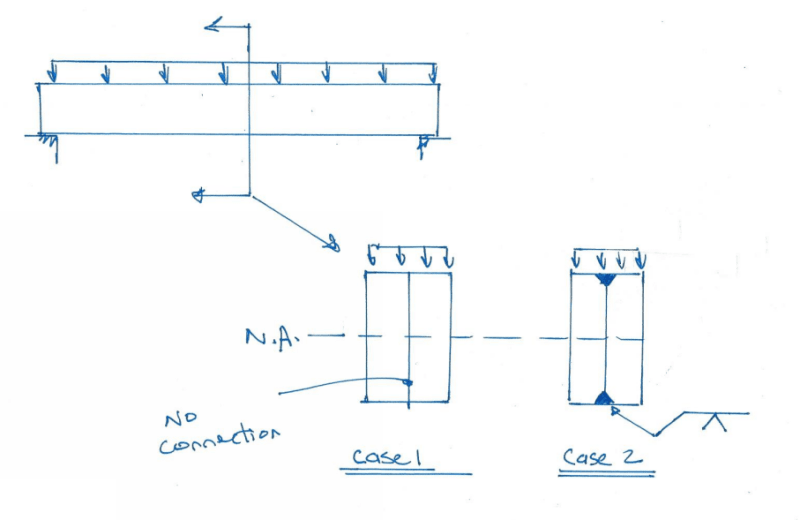
I understand there's no shear flow for situations like a flitch beam where load is applied to all components and all components are supported independently at the ends.
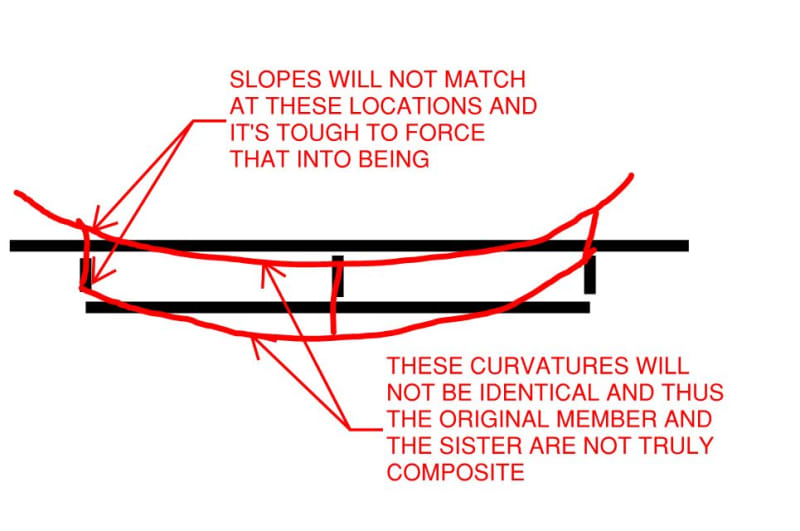
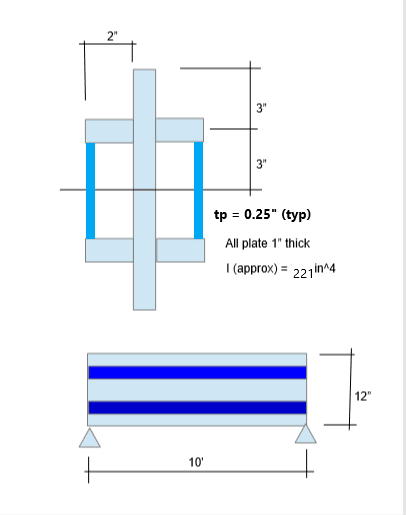
I've seen a situation where there was a simply supported wood beam that was damaged at midspan. To add strength to the beam, the engineer sistered on two 2x's, one on each side of the beam, bolted. However, the 2x's did not extend all the way to the supports. Also, the load was applied only to the beam, not the sistered 2x's. The members shared the same Neutral axis. So in this situation, is there still no shear flow? How does load get transfered to the 2xs? How do we insure that the 2xs will add strength rather than just add dead load to the main beam? Right now I'm thinking you can't just transfer vertical shear through the bolts to the 2xs because they're not supported independently at the ends.
Thanks in advance for your time.
There's a lot of great discussion regarding shear flow of members that share the same Neutral Axis. From the thread responses, it seems that there is no shear flow between the members that share a neutral axis.
I understand there's no shear flow for situations like a flitch beam where load is applied to all components and all components are supported independently at the ends.
I've seen a situation where there was a simply supported wood beam that was damaged at midspan. To add strength to the beam, the engineer sistered on two 2x's, one on each side of the beam, bolted. However, the 2x's did not extend all the way to the supports. Also, the load was applied only to the beam, not the sistered 2x's. The members shared the same Neutral axis. So in this situation, is there still no shear flow? How does load get transfered to the 2xs? How do we insure that the 2xs will add strength rather than just add dead load to the main beam? Right now I'm thinking you can't just transfer vertical shear through the bolts to the 2xs because they're not supported independently at the ends.
Thanks in advance for your time.