shockey25
Mechanical
- Jul 23, 2020
- 1
Hello All
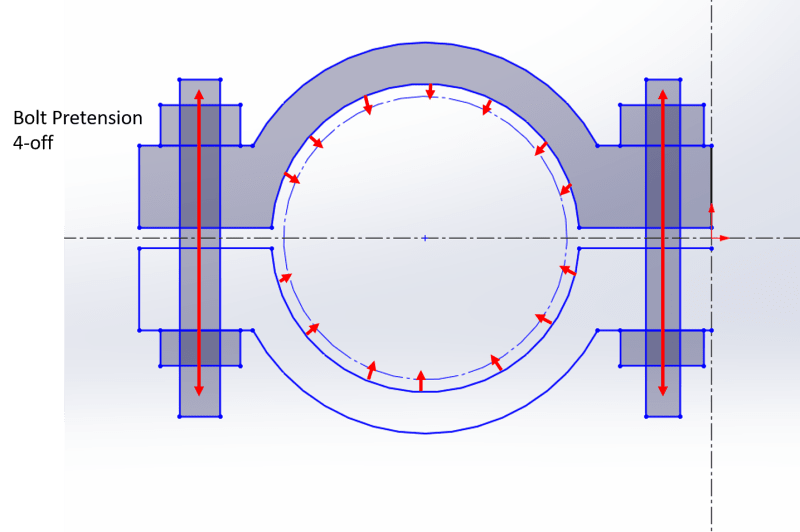
I have a two fold question/challenge regarding a split clamp. What I mean by a split clamp is two piece clamp per attached image.
The initial question I have is regarding correct calculation of the inward force exerted on the pipe, how is the inward force correlated to the tension in the bolts?
I can provide the bolt material - B7, yield strength ~724MPa, assumed Cof ~0.2 and aiming to use no more that 80% of yield. M20s /3/4UNCs provisionally but could increase
The second part of the challenge is connecting a lever arm into this clamp and rotating it, aiming to put a twist into the pipe, assuming it is clamped at the other end. In this scenario.I wish to ensure that my clamping force is sufficient to prevent the pipe slipping. I would intend to place a rubber pad between the pipe and the clamp wall to increase and normalise the COF. In this case I'm looking to find the relationship between the torque applied to induce a 2 degree twist in the pipe (8,126Nm) and whether the clamping force with the benefit of the high COF rubber will prevent it moving under this applied torque
Thanks
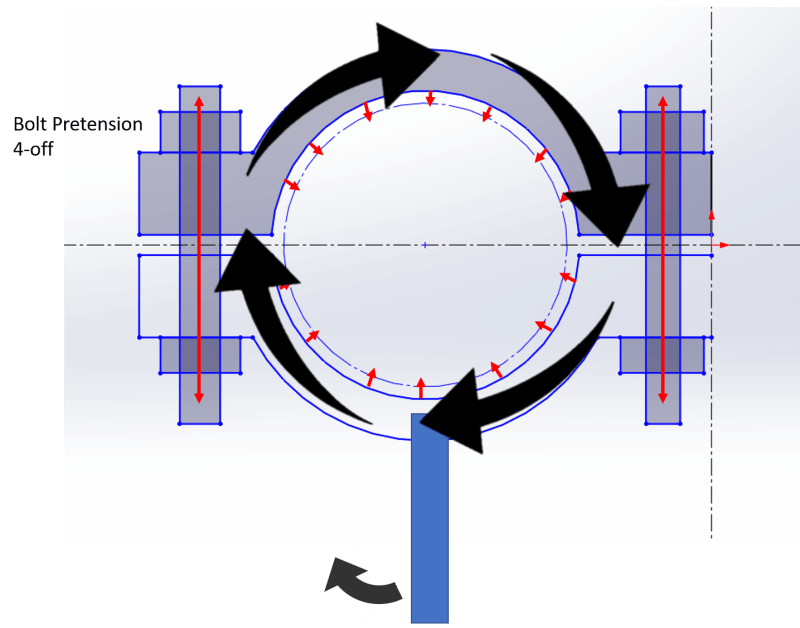

I have a two fold question/challenge regarding a split clamp. What I mean by a split clamp is two piece clamp per attached image.
The initial question I have is regarding correct calculation of the inward force exerted on the pipe, how is the inward force correlated to the tension in the bolts?
I can provide the bolt material - B7, yield strength ~724MPa, assumed Cof ~0.2 and aiming to use no more that 80% of yield. M20s /3/4UNCs provisionally but could increase
The second part of the challenge is connecting a lever arm into this clamp and rotating it, aiming to put a twist into the pipe, assuming it is clamped at the other end. In this scenario.I wish to ensure that my clamping force is sufficient to prevent the pipe slipping. I would intend to place a rubber pad between the pipe and the clamp wall to increase and normalise the COF. In this case I'm looking to find the relationship between the torque applied to induce a 2 degree twist in the pipe (8,126Nm) and whether the clamping force with the benefit of the high COF rubber will prevent it moving under this applied torque
Thanks

