flyforever85
New member
Hi all,
I am an aerospace engineer and recently I analyzed a complex structure and submit the report to the FAA for evaluation.
Some premises:
- the structure was in aluminum;
- I applied ultimate loads since it was a crash conditions;
- All the Von Mises results came back well below yield;
- I calculated all the UMS as stress(Von Mises from FEM)/Stress(Ultimate)-1
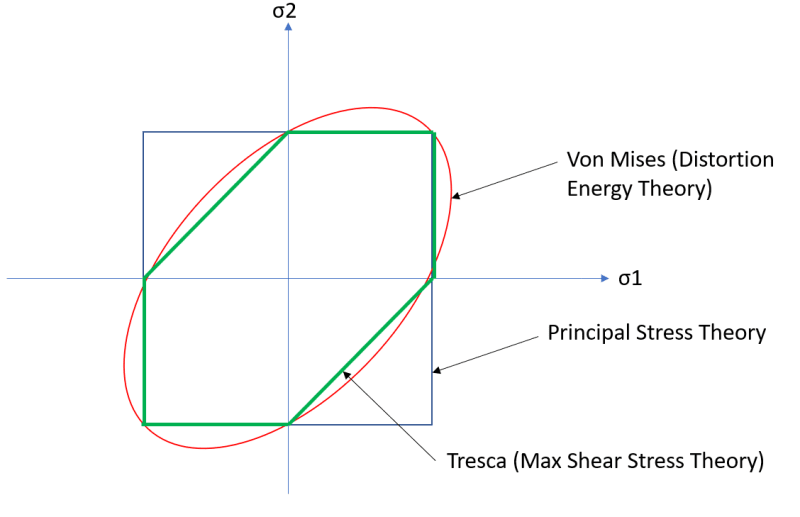
The FAA came back saying they will accept the report as it is with no concern although I will have to use the max principle stress criteria from now on instead of Von Mises. I think Von Mises is more conservative than the max principle stress, at least at lower sigma2 values. What am I missing?
I am an aerospace engineer and recently I analyzed a complex structure and submit the report to the FAA for evaluation.
Some premises:
- the structure was in aluminum;
- I applied ultimate loads since it was a crash conditions;
- All the Von Mises results came back well below yield;
- I calculated all the UMS as stress(Von Mises from FEM)/Stress(Ultimate)-1
The FAA came back saying they will accept the report as it is with no concern although I will have to use the max principle stress criteria from now on instead of Von Mises. I think Von Mises is more conservative than the max principle stress, at least at lower sigma2 values. What am I missing?

![[lol] [lol] [lol]](/data/assets/smilies/lol.gif)