Marc Rogue
Structural
Hello guys,
Just recently embarked into wood design. Reading up on a wood design book I came across the design of a hip beam but the calcs proposed in the book don’t jive well with me and I wanted to get someone else’s opinion. I know books get revisions so it should be ok but the problem is their solution yields more total load than it’s actually there. Please look at the images and let me know your thoughts on it.
Thank you
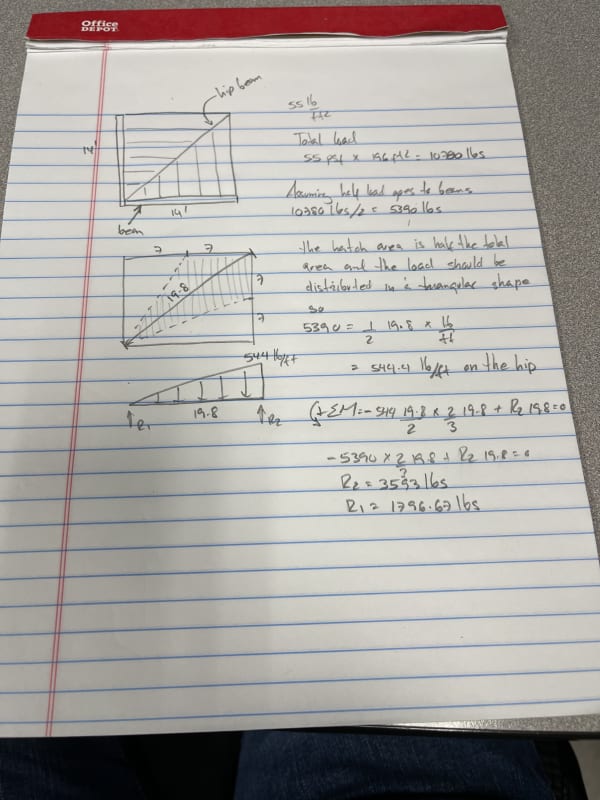
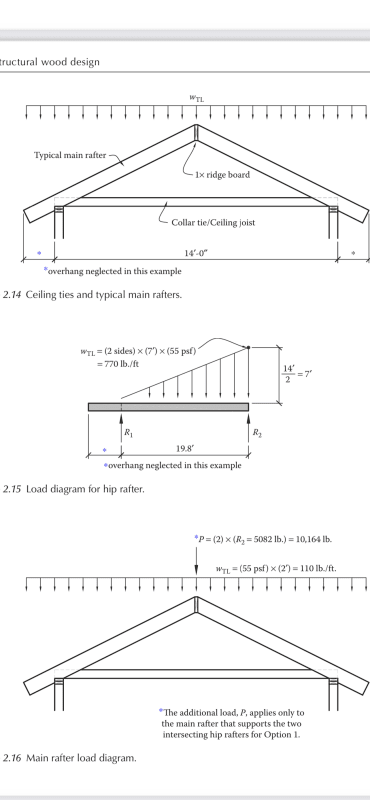
Just recently embarked into wood design. Reading up on a wood design book I came across the design of a hip beam but the calcs proposed in the book don’t jive well with me and I wanted to get someone else’s opinion. I know books get revisions so it should be ok but the problem is their solution yields more total load than it’s actually there. Please look at the images and let me know your thoughts on it.
Thank you


