thread507-457014
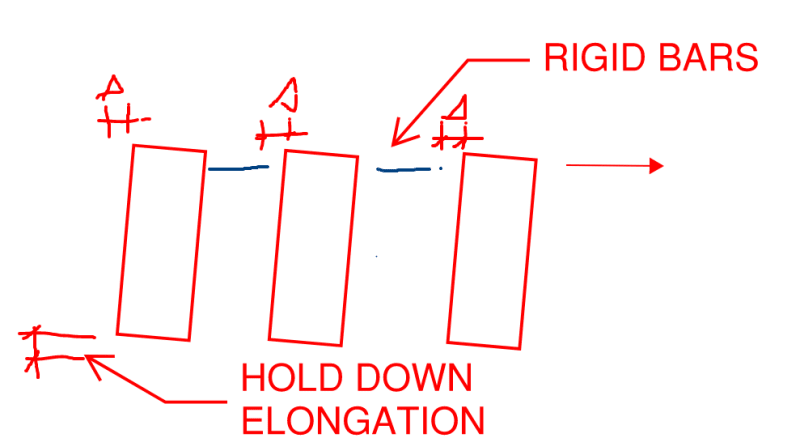
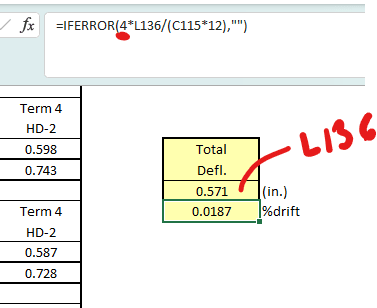
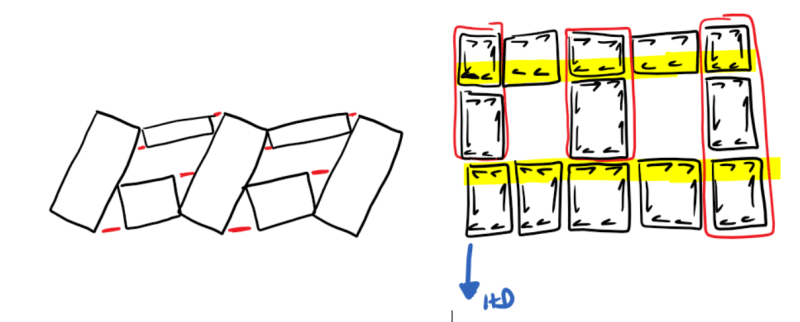
bones - I hope you're around today. Ever hear back about this from anyone? I've got a building with lots of windows all around that are driving pier widths way down. There's enough that using strong walls for their better stiffness isn't really an option - I'd just have strong walls and roof trusses. So I'm trying to drill down deeper into this deflection calculation and, though the data appears to track nicely with the hystersis and backbone plots, I can't rationalize the application of hold down deflections to piers without hold downs.
bones - I hope you're around today. Ever hear back about this from anyone? I've got a building with lots of windows all around that are driving pier widths way down. There's enough that using strong walls for their better stiffness isn't really an option - I'd just have strong walls and roof trusses. So I'm trying to drill down deeper into this deflection calculation and, though the data appears to track nicely with the hystersis and backbone plots, I can't rationalize the application of hold down deflections to piers without hold downs.