Pretty Girl
Structural
- Nov 22, 2022
- 73
The following equation to get the moment of the compression force (Mc) is mentioned in the "Reinforced Concrete Design to Eurocodes" by prab bhatt on page 353.
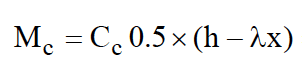
My question is:
Is the "0.5" number mentioned in that is the neutral axis? can we use 0.7 instead of 0.5? I noticed if we use higher number for that, we can reach higher moment resistances.
But I'm not sure if the "0.5" is for the neutral axis or not.
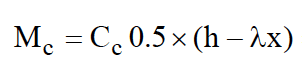
My question is:
Is the "0.5" number mentioned in that is the neutral axis? can we use 0.7 instead of 0.5? I noticed if we use higher number for that, we can reach higher moment resistances.
But I'm not sure if the "0.5" is for the neutral axis or not.
