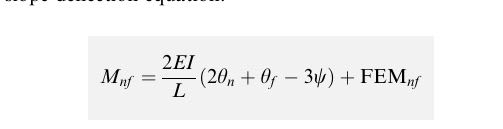Tygra_1983
Student
- Oct 8, 2021
- 121
Hi all,
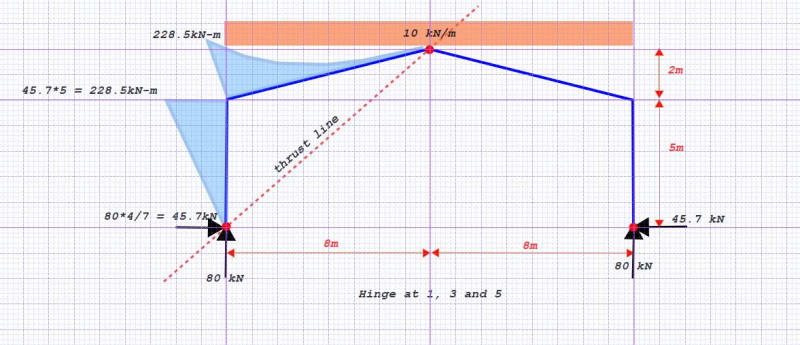
I am trying to solve the following Portal Frame:
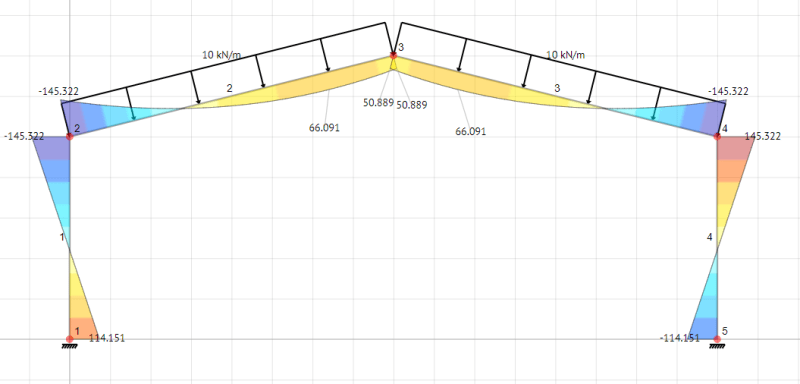
I am using BeamGuru to validate my hand calcs and they give the respective moments that are shown in the image.
The dimensions are: columns 5 metres high, and rafters that are 8.2462 metres long. The frame is 16 metres long (8 metres halfway). The peak of the frame is 7 metres.
However, when I do my hand calcs I am getting very different results and I don't know why.
Here are my calculations in Octave:
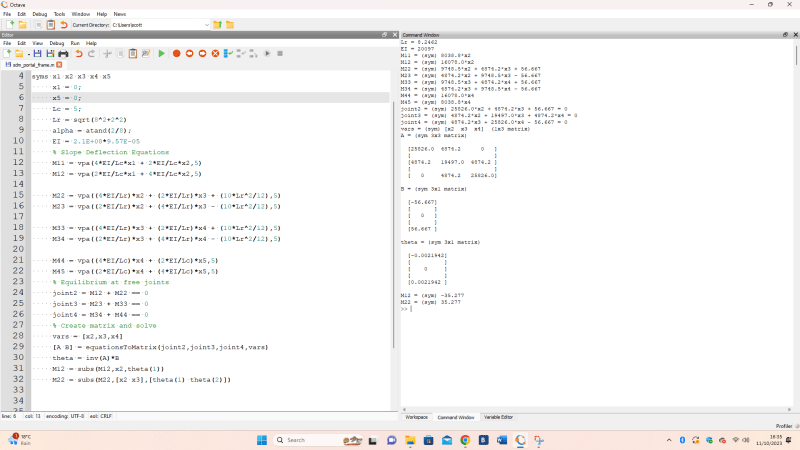
As you can see, I am getting moments at joint 2 of 35.227 kNm. This is way off the results in BeamGuru. I cannot see what error I am making. So could someone please help?
Many thanks!
I am trying to solve the following Portal Frame:

I am using BeamGuru to validate my hand calcs and they give the respective moments that are shown in the image.
The dimensions are: columns 5 metres high, and rafters that are 8.2462 metres long. The frame is 16 metres long (8 metres halfway). The peak of the frame is 7 metres.
However, when I do my hand calcs I am getting very different results and I don't know why.
Here are my calculations in Octave:

As you can see, I am getting moments at joint 2 of 35.227 kNm. This is way off the results in BeamGuru. I cannot see what error I am making. So could someone please help?
Many thanks!