jochav52802
Structural
Good Day!
Any idea why AISC's Design Guide-9 calculates warping stresses within it's design examples that are defined as "torsionally-pinned"?
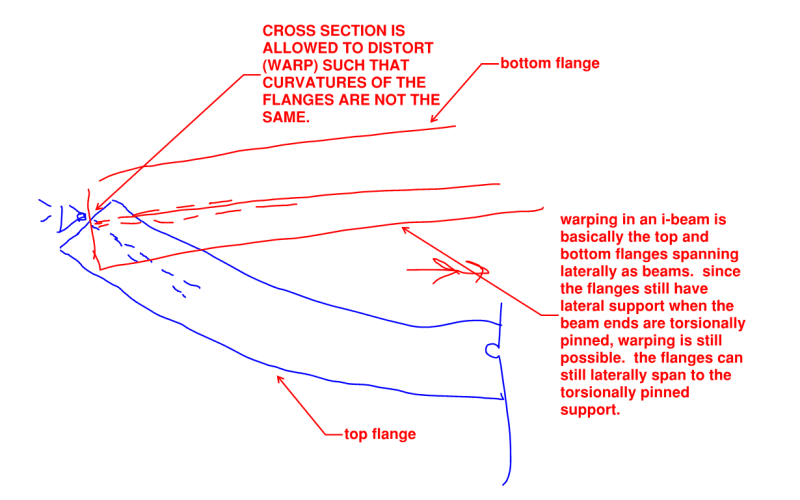
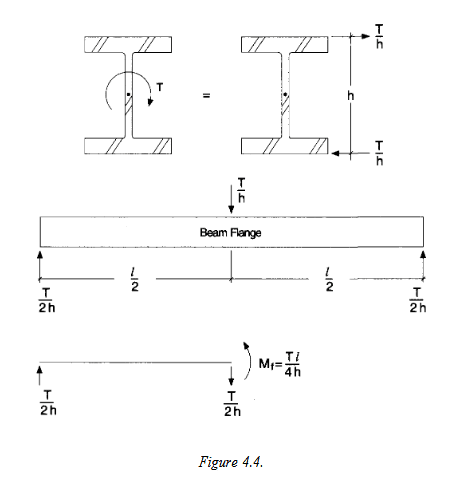
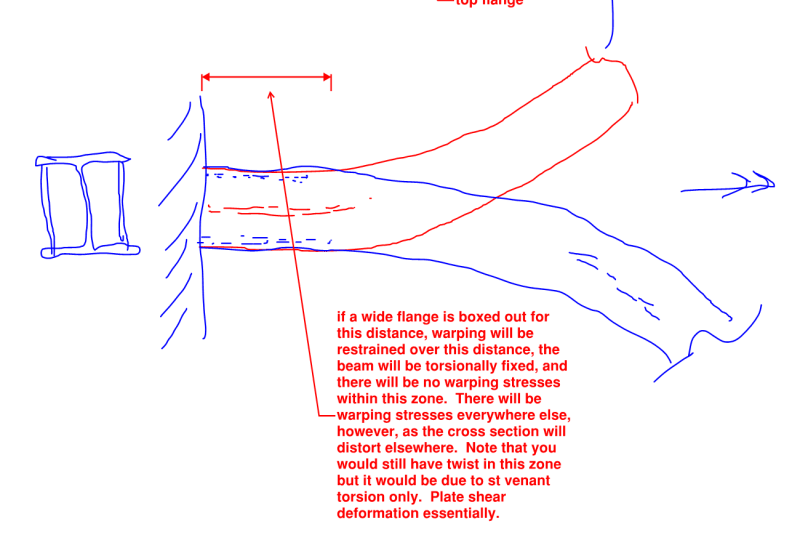
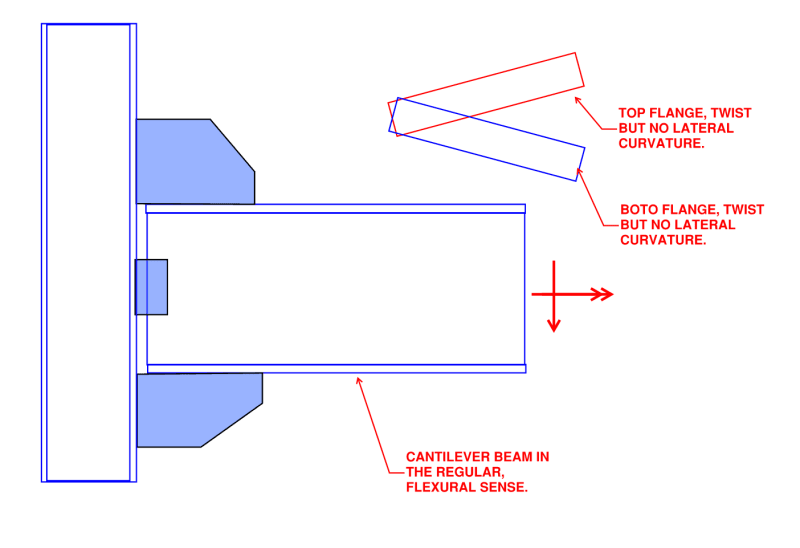
That design guide says that warping stresses can't develop when the section is not restrained from warping, as would be the case when it's "torsionally-pinned". So why does example 5.1 and 5.4 calculate those warping stresses and then add them to the regular flexural and pure torsion stresses?
Many thanks for any support here!
Any idea why AISC's Design Guide-9 calculates warping stresses within it's design examples that are defined as "torsionally-pinned"?
That design guide says that warping stresses can't develop when the section is not restrained from warping, as would be the case when it's "torsionally-pinned". So why does example 5.1 and 5.4 calculate those warping stresses and then add them to the regular flexural and pure torsion stresses?
Many thanks for any support here!